47766 Zadanie4Piaseckiego ekonometria2byEOP

WERS]A UAKTUALNIONA

4. Przetestować na poziomie 5% hipotezę, że 2.5 < (}>a^< 3 wykorzystując następujące liczby:

1 > ^

,    a    Ą

Sr = 1.3. C(X.Y) 12.6. A = 10.2. A, =2.8. n=50

Po pierwsze mam lepszą wersję bardziej zprecyzowaną jeśli chodzi o alfa

3 wykorzystując

Jeśli poziom istotności 5% to ufności 95% zatem alfa = 0,05 Z tablic inaczej powinno być.

No i ten magiczny wzór na var x

na var x to ja znak taki    _

varx = cov(x,x) = V (xi-x)² = V xi²

a tu chyba chodziło o S* (x) =

2.    cov(x,y)¹²'⁶

Ą²’⁸

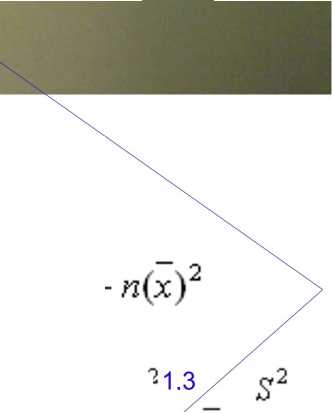
-a* - ^s‘

^A “ tóiT

var X

No i mamy pierwszy zonk s2(X)= 12,6/2,8=4,5 wychodzi s2b1 =1,3/(50*4,5)=0,005777

50*4,5

sb1 =0,0760

ale zajżycie do kartki ze wzorami bo można zamiast Czebyszewa zrobić kwartylami t-Studenta i k wyjdzie inne tj. nie 4,47 tylko 2,0106 Z nierówności Czebyszewa (tożsamej z prawem k-sigm) korzysta się gdy błąd

No i przedział dla b1 to b1 należy do (b1-4,47*sb1;b1-4,47*sb1)

4,47 z nierówności czebyszewa gdy ufność 95%

nie ma rozkładu normalnego, gdy ma - stosuje się kwartyle rozkadu t-Studenta. Ale pamiętajcie, że wtedy t( l-(alfa/2);n-2) więc na poziomie ufność 0,95 z tablicy weźmiemy od 0,975. Przykładowo dla dla n=20 i istotności = 0,20 (ufności 80%) t-Studenta będzie ((l-0,20/2;20-2)=t(0,9;18)=l,33