48658 skanowanie0064

„    1    ,    v cor

H — —ar. v$mat,    t = — =» •—I

2    aa

jest równe

o)²r² F r²'4mg

2H 2mr 2-10,3J^?r Stąd siła naciągu nici S wynosi

= 0,097g

S = m (g-0,091 g) = 0,903 mg N

Przykład 6.16. Na rysunku 6.16 pokazano układ trzech kół i ciężarek A o masie m kg. Koło o masie m kg toczy się bez poślizgu po równi pochyłej

0    kącie pochylenia a. Współczynnik tarcia tocznego wynosi / Stały moment M N • m jest przyłożony do koła o masie 2m i promieniu 2r, obracającego się względem osi O. Z kołem tym jest połączone koło o masie m i promieniu r (rys. 6.16). Wyznaczyć przyspieszenie kątowe e₂ oraz moment układu M_zrei0

1    moment bezwładności układu I_zred0 zredukowany do osi O. W chwili początkowej układ znajduje się w spoczynku.

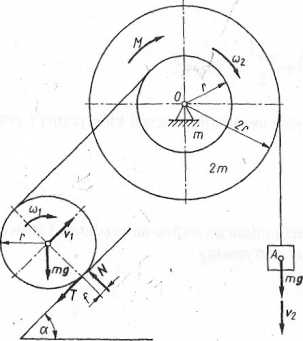
Rys. 6.16. Do przykładu 6.16

Rozwiązanie. W chwili początkowej prędkości liniowe krążka ruchomego i ciężarka oraz prędkości kątowe kół są równe zeru. Zatem energia kinetyczna

Załóżmy, że prędkości końcowe krążka ruchomego i ciężarka są równe v_t i v₂> a prędkości kątowe kół co₁ i co₂ (rys. 6.16). Energia kinetyczna końcowa

1,1 mr² ,    1    , x% (mr² 2m‘4r^a&*«&-

E =    — + —-—\oĄ =

= ~ oĄ H --+-~-H- 4 mr² + ~ mr²^ = ^mr²(Ą

gdzie zależności między prędkościami liniowymi v_t i v₂ a prędkościami kątowymi a)₁ i co₂ są równe

co_tr = —co₂r, v₂ = co₂'2r, co₂r = co₁’2r \

Pracę wykonują siły ciężkości oraz momenty M i Nf V

M(p₂—m^sina-Sj — Nf<p_x +mgs₂ — ę₂(^M—mg-^sina—N^+2mgr\

r    q>₂

gdzie: s₁ = <p2~2> <Pi ⁼    s₂ = ą>₂*2r, N = mgcosa

Po podstawieniu wzorów na końcową energię kinetyczną £₂ i pracę t^do równania przedstawiającego zasadę równoważności energii kinetycznej i pracy otrzymamy

■.-r-r-mr²CQ²—0 = q>'₂( M — mg~-sina — mg cos a+ 2mgr .16 ^!‘\ 2

Po zróżniczkowaniu obu stron tego równania względem czasu

„71    , . dw₇    dq>₇ (    r .    f

2-—-_/rmr co₂—-— = ,    ( M—mg--sina—mg—cosa+2mg

16    dt    dt \    2    2

Stąd

M—mg^sintt—mg—cosa+2mgr —    ^ . t '    ^

Moment układu zredukowany do osi 0 wynosi

Y    f

Mzredo ⁼ M—mg—sina—ro#ycosa + 2mgr N-m

151