50056 Untitled Scanned 06

- 12 -

Charakterystyczną cechą sygnałów cyfrowych jest to, że ich wartości należą do zbioru przeliczalnego. Sygnały przyjmujące jedynie dwie wartości, nazywają się sygnałami binarnymi (dwuwartościowymi), przyjmujące trzy wafctości - trójwar-. tościowymi itd.

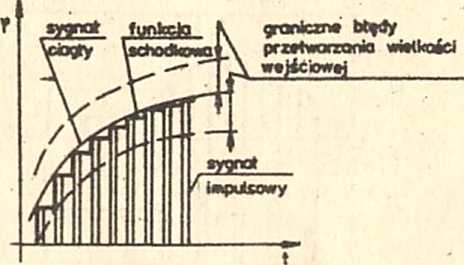
Rys.1.4. Porównanie sygnału ciągłego i impulsowego

Jednym z zastosowań sygnałów binarnych jest przekazywanie informacji o wielkościach binarnych. Podobnie, sygnały trójwartościowe wykorzystywane mogą byó do przekazywania informacji o wielkościach trójwartościowych, a sygnały wielowartoś-ciowe do przekazywania informacji o wielkościach występujących w procesach dyskretnych.

Sygnały wielowartościowe wykorzystywane są również do e-proksym.acji przebiegów ciągłych. Przekazywanie informacji o przebiegu ciągłym za pomocą sygnału wielowartościowego związane jest z przypisaniem kolejnym zakresom wertości wielkości ciągłej kolejnych wartości sygnału wielowartościowego. Operacja ta nazywa Bię kwantowaniem w poziomie - rys.1.5a. Zamiana sygnału ciągłego na wielowartościowy nie powoduje zniekształcenia przekazywanych informacji Jeżeli przebieg sygnału wielowartościowego nie wykracza poza granice określone przez graniczne błędy przetwarzania.

Sygnały wielowartościowe w postaci przebiegu schodkowego (jak na rys.1.5a) wykorzystywane są rzadko. Najczęściej występują ono w postaci zakodowanej za pomocą kilku sygnałów binarnych. Przykład wielowartościowego sygnału kodowanego równolegle (za pomocy kilku równolegle przesyłanych sygnałów binarnych), odpowiadającego sygnałowi y(t) wg rys.1„5a, pokazano na ry8.1.5b. Zastosowany kod podaje tablica na ryB.1.5c.

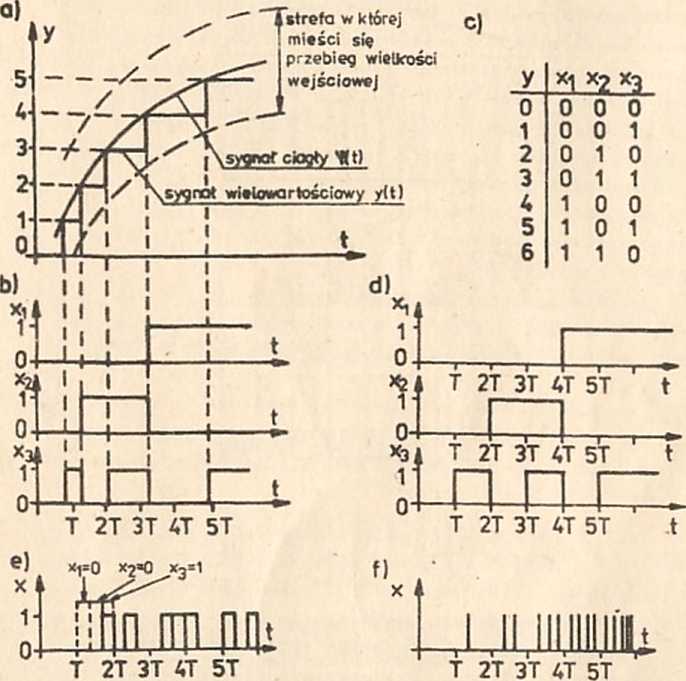
Rys.1.5. Sygnały cyfrowe wielowartościowe: a) niekodowa-nv; b) kodowany równoległej c) przykład tablicy kodowejj d) dyskretny kodowany równoległej e) dyskretny kodowany szeregowo z wykorzystaniem kodu dwójkowegoj f J dyskretny kodowany szeregowo z wykorzystaniem kodu unitarnego

Oprócz wielowartodciowych sygnałów ciągłych (ciągłych w czasie), wykorzystywane są również wielowsrtoćciowe sygnały próbkowane, zwane również dyskretnymi (sygnały kwantowane w poziomie i w czasie). Fodobnie Jak w przypadku sygnałów impulsowych, można wykazać, że odpowiednio przeprowadzona dys-