50682 Str082

160 S. licjtby pirrwwe i rorktsd nu raynnłki

(a) znajdujemy liczbę całkowito b. która spełnia: b e g (mod p) oraz b $ 1 (mod nip), Wtedy NWD(b% 11) = 1 i b*~^l ==    ¹ (mod p). Ale g"^-1 _n,_e

przystaje do 1 modulo p, gdyż n — 1 nie dzieli się przez rząd p — 1 liczby o Zatem b*~¹ ^1 (mod /?), a więc (1) nic może zachodzić. To kończy dowód twierdzenia.

Przykład 2. Liczba n = 561 = 311 17 jest liczbą Carmichaela, gdyż 560 dzieli się przez 3-1, 11-1 i 17-1. W ćwiczeniach zobaczymy, że jest to najmniejsza liczba Carmichaela.

Twierdzenie 5.1.3. Każda liczba Carmichaela jest iloczynem co najmniej trzech różnych liczb pierwszych.

Dowód. Na mocy twierdzenia 5.1.2 wiemy, że liczba Carmichaela n musi być iloczynem różnych liczb pierwszych. Wystarczy zatem wykluczyć możliwość, że n = pq jest iloczynem dwóch różnych liczb pierwszych. Przypuśćmy, że p < q. Wtedy, gdyby liczba n była liczbą Carmichaela, mielibyśmy n — 1=0 (mod q — 1), na mocy części (b) twierdzenia 5.1.2. Ale n — 1 = p(q — 1 + + 1) - 1 = p - 1 (mod ^ — 1), a ta liczba nie przystaje do 0 modulo q — 1, ponieważ 0 < /z — 1 < <7 - 1. To kończy dowód.

Uwaga. Bardzo niedawno Alford, Granvillc i Pomcrancc udowodnili, że istniej e nieskończenie wiele liczb Carmichaela; por. komunikat Granville’a w No-tices of the Amer. Math. Soc., 1992, 39, s. 696-700.

Liczby pseudopierwsze Eulera. Niech n będzie liczbą nieparzystą i niech

(b\

I — I oznacza symbol Jacobiego (zob. podrozdział 2.2). Zgodnie z twierdzeniem 2.2.2, jeśli n jest liczbą pierwszą, to

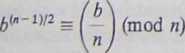
(2)

dla dowolnej liczby całkowitej b. Z drugiej strony, jeśli liczba n jest złożona, to z ćwiczenia 21 w podrozdziale 2.2 wynika, że co najmniej 50% wszystkich 6e(Z//iZ)* nie spełnia (2). Z tych dwóch faktów możemy otrzymać efektywny probabilistyczny test wykazujący, czy duża nieparzysta liczba naturalna n jest liczbą pierwszą. Rozpoczniemy od następującej definicji.

Definicja. Jeśli n jest nieparzystą liczbą złożoną i b jest taką liczbą całkowitą, że NWD(n, b) — 1 oraz zachodzi (2), to liczbę n nazywamy liczbą pseudopierwszą Eulera przy podstawie b.

Twierdzenie 5.1.4. Jeśli n jest liczbą pseudopierwszą Eulera przy podstawie b, to jest liczbą pseudopierwszą przy podstawie b.

powód. Musimy pokazać, że jeśli zachodzi (2), to zachodzi też (I). Ale to jest oczywiste po podniesieniu do kwadratu obu stron kongrucncji (2).

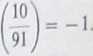
przykład 3. Twierdzenie odwrotne do twierdzenia 5.1.4 jest fałszywe. W przykładzie 1 zobaczyliśmy, że liczba 91 jest pseudopierwszą przy podstawie 3. Jednakże 3⁴⁵ s 27 (mod 91), a więc (2) nie zachodzi dla n - 91, b = 3. (Zauważmy, że podniesienie b do wysokiej potęgi modulo 91 jest łatwe, jeśli znamy rząd b w (Z/91Z)*; ponieważ 3⁶ s 1 (mod 91), to natychmiast widzimy, że 3⁴⁵ = 3³ (mod 91)). Przykładem podstawy, przy której 91 jest liczbą pseudopierwszą Eulera, jest 10, ponieważ 10^ = 10³ = -1 (mod 91) oraz

przykład 4. Łatwo pokazać, że każda złożona liczba nieparzysta n jest liczbą pseudopierwszą Eulera przy podstawie ±1; w dalszym ciągu wykluczymy te dwie „trywialne” podstawy b.

Możemy teraz opisać test pierwszości Soloraya-Strassena. Przypuśćmy, że n jest nieparzystą liczbą naturalną i chcemy wiedzieć, czy n jest liczbą pierwszą czy złożoną. Wybieramy losowo k liczb 0 < b < tl Dla każdej takiej liczby b najpierw obliczamy obie strony kongruencji (2). Do obliczenia lewej strony ó⁽ⁿ~^1)/2 potrzeba 0(log³n) operacji na bitach, wykorzystując metodę iterowanego podnoszenia do kwadratu (twierdzenie 1.3.6); do obliczenia symbolu Jacobiego po prawej stronie również potrzeba 0(log³n) operacji na bitach (zob. ćwiczenie 17 w podrozdziale 2.2). Jeżeli obie strony nie przystają do siebie modulo n, to wiemy, że n jest liczbą złożoną i kończymy test. W przeciwnym razie bierzemy następną liczbę b. Jeśli (2) zachodzi dla k losowo wybranych b, to prawdopodobieństwo tego, że n jest liczbą złożoną pomimo pomyślnego przejścia przez wszystkie testy, wynosi co najwyżej 1/2*. Zatem test Solovaya-Strassena jest algorytmem probabilistycznym prowadzącym do konkluzji, że liczba n jest złożona, lub do konkluzji, że jest ona „prawdopodobnie” pierwsza.

Zauważmy, że dla liczb pseudopierwszych Eulera nie ma liczb analogicznych do liczb Carmichaela: każda liczba złożona n nie przechodzi testu (2) dla co najmniej połowy możliwych podstaw b.

Liczby silnie pseudopierwsze. Omówimy teraz jeszcze jeden test pierwszości, który pod pewnym względem jest nawet lepszy od testu Solovaya-Strassena, opartego na definicji liczb pseudopierwszych Eulera. Jest to test Millera-Rabina, oparty na pojęciu liczb „silnie pseudopierwszych”, które zostaną teraz zdefiniowane. Załóżmy, że n jest dużą nieparzystą liczbą naturalną i be (Z/ni)*. Przypuśćmy, że n jest liczbą pseudopierwszą przy podstawie b, czyli bⁿ~^l = 1 (mod n). Pomysł, na którym oparte jest pojęcie liczby silnie pseudopierwszej, polega na tym, że jeśli będziemy „wyciągali pierwiastek kwadratowy" z obu stron tej