55836 Str085

166 S Liczby pierwszo i rozkłsd nu czynniki

(lj_P²7V - (*. ft \ X ■'.....K^hP n). Zgodnie z lematem 1, liczba tych b modu|₀

które spełniają kongrucncję //' ¹ s 1 (mod p²), wynosj d~NWD(p(p - 1). n - I). Ponieważ p\n_% to pj(n - 1 i stąd pfd. Zatem największym takim d może być p - 1. Stąd wynika, że stosunek liczby tych b w przedziale od 0 do n, które nic są podzielnc przez p² i spełniają kongrucncję ó" ¹ s 1 (mod p²) do liczby wszystkich takich b z tego przedziału, jest nic większy od

p-1    1    1

p²- 1    p+ 1 ^ 4’

Ponieważ stosunek tych b w przedziale od 0 do w, które spełniają kongrucncję bⁿ~¹ = 1 (mod n), do wszystkich b jest co najwyżej jeszcze mniejszy, więc stąd otrzymujemy wniosek, że liczba n jest liczbą pseudopierwszą przy podstawie b dla co najwyżej 1/4 wszystkich b takich, żeOcócn. To dowodzi twierdzenia w przypadku (i). (Uwaga. To ograniczenie górne 25% jest w istocie przyjmowane w przypadku (i) dla n = 9, tzn. liczba 9 jest (silnie) pseudopierw-sza dla dwóch spośród 8 możliwych podstaw 6. mianowicie b = ± 1.)

Przypadek (ii). Przypuścimy następnie, że n jest iloczynem dwóch różnych liczb pierwszych p i q: n = pq. Niech p — 1 = 2⁵    gdzie /' jest liczbą

nieparzystą, i niech q— 1 = 2^a 't", gdzie t" też jest liczbą nieparzystą. Bez straty ogólności możemy założyć, że r' ^ 5". Po to, by element óe(Z/nZ)* był podstawą, przy której liczba n jest silnie pseudopierwszą, musi zajść jedna z następujących dwóch możliwości: (1) b¹ = 1 (mod p) oraz b* = 1 (mod q) lub (2) b^Vt = — 1 (mod p) oraz b^2rt = — 1 (mod q) dla pewnej liczby r takiej, że 0 Ąr <s. Zgodnie z lematem 1 liczba takich b, dla których zachodzi pierwsza możliwość, jest iloczynem NWD(t, t') (czyli liczby reszt modulo p) przez NWD(t, f") (czyli liczby reszt modulo q\ który na pewno nie jest większy od t'l". Zgodnie z lematem 2 dla każdej liczby r < min(5', $") = s' liczba takich 6, dla których b^Vt = -1 (mod n) wynosi 2^r NWD(t, /') • 2^r NWD(t, t") < < Ponieważ mamy n — 1 > (p(ń) = 2^{a +,} 't't", więc stąd wynika, że stosunek liczby tych b, 0 <b <n, dla których liczba n jest silnie pseudo-pierwsza przy podstawie 6, do wszystkich liczb b w tym przedziale, wynosi co najwyżej

t’t" + t^hf + 4/'/" + 4²/'f" + ... + 4^a'~¹/7^//    , „/    4'' - 1 \

-² ' ' (* + 4_i )■

Jeśli s" > s\ to ten ostatni ułamek wynosi co najwyżej /2    4*'\    2    1    1

2~²* ¹(^^+-3~)^^³y ⁺ "6⁼⁼'4’ Zauważmy następnie, że jeśli s' =

to jedna z nierówności NWD(t,    NWD(l, /") < /" musi być ostra.

Gdyby bowiem /'|/ i /"|/, to z kongruencji 72 - 1 = 2'/ = pq — 1 = q — 1 (mod pi wynikałoby, że    - 1 = czyli /'|/". Podobnie mielibyśmy /"|/\ a to

oznacza, że t' = f", czyli p — q, co przeczy założeniu. Zatem jeden z tych

dwóch największych wspólnych dzielników jest ostro mniejszy od l' lub _{a w}jęc musi być co najmniej 3 razy mniejszy (bo l' \ t" v\ nieparzyste). Zatem

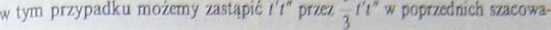
niach liczby tych b, które spełniają każdy warunek wystarczający do tego, by liczba n była silnie pseudopierwszą przy podstawie b. To prowadzi do następującego oszacowania z góry stosunku liczby tych b, 0 < b < n, dla których n jest silnie pseudopierwszą przy podstawie b, do liczby wszystkich możliwych b:

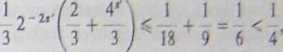
czego należało dowieść. To kończy dowód twierdzenia w przypadku (ii).

Przypadek (iii). Wreszcie przypuśćmy, że n jest iloczynem więcej niż dwóch różnych liczb pierwszych: n = p_tp₂ ■... ■ p_k1 k ź 3. Niech p, - 1 = = 2*^Jtj, gdzie liczby ł_} są nieparzyste, i powtórzmy rozumowanie z przypadku (ii). Bez straty ogólności możemy założyć, że r, ^ s_} jest najmniejszą z liczb Sy Otrzymamy następujące oszacowanie z góry stosunku liczby tych podstaw b, przy których liczba n jest silnie pseudopierwszą, do liczby wszystkich możliwych b:

bo k ^ 3 w przypadku (iii). To kończy dowód twierdzenia 5.1.7. ^{1 2}

Uwagi:

1

   W rzeczywistości nikt w praktyce nie musi wybierać bardzo wielkiej liczby podstaw b, by być prawie pewnym, że liczba n jest pierwsza, jeśli jest silnie pseudopierwszą względem wszystkich tych podstaw. Na przykład obliczono, że istnieje tylko jedna liczba złożona mniejsza niż 2,5 - lO¹⁰, mianowicie 3215031751, która jest silnie pseudopierwszą przy czterech podstawach: 2, 3, 5, 7.

2

   Poleganie na teście probabilistycznym nie satysfakcjonuje nas w pełni. Pomimo zapewnienia Emila Borela, zacytowanego na początku tego rozdziału , byłoby dobrze mieć szybką metodę dowodzenia, że dana liczba n jest rzeczywiście pierwsza (zwłaszcza, gdy jest to z jakichś praktycznych czy teoretycznych względów ważne, by wiedzieć, że ta szczególna liczba n jest pierwsza). Gdybyśmy na przykład wiedzieli, że istnieje jakaś względnie mała liczba B (zależna od wielkości n) taka, że jeśli n jest złożona, to istnieje pewna podstawa b < B, dla której liczba n nie jest silnie pseudopierwszą.