83423 Str101

• W 5. Liczby pierwsze i foaktad im czynniki

2. (u) Przypuśćmy, że x jest liczbą rzeczywistą, której rozwinięcie na ułamek łańcuchowy składa się z liczby całkowitej a, powtarzającej się w nieskończoność:

Jaką liczbą jest x (w możliwie prostej postaci)?

(b) Udowodnij, żc jeśli a = 1 w punkcie (a), to x jest liczbą wyrażającą stosunek „złotego podziału”, a licznik i mianownik kolejnych reduk-tów są liczbami Fibonaccicgo.

3.    Rozwiń liczbę e na ułamek łańcuchowy i spróbuj odgadnąć regułę rządzącą kolejnymi liczbami a_t.

4.    Wyjaśnij, dlaczego w algorytmie faktoryzacji korzystającym z ułamków łańcuchowych nic musimy włączać do bazy rozkładu B liczb pierwszych

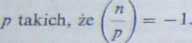
5. Wzorując się na przykładach 2 i 3, zastosuj algorytm faktoryzacji korzystający z ułamków łańcuchowych, by rozłożyć na czynniki następujące licz

by: (a) 9509; (b) 13561; (c) 8777; (d) 14429; (e) 12403; (f) 14527; (g) 10123; (h) 12449; (i) 9353; (j) 25511; (k) 17873.

Bibliografia

1.    Davenport H.: The Higher Arithmelic. Wyd. 5, Cambridge University Press 1982.

2.    Knuth D.: The Art of Computer Programming. T. 2, Addison-Wesley 1973.

3.    Lehmer D.H., Powers R.E.: On factoring large numbers. Buli. Amer. Math. Soc., 1931, 37, s. 770-776.

4.    Morrison MA., Brillhart J.: A method of factoring and the factorization of F₇. Math. Comp., 1975, 29, s. 183-205.

5.    Pomerance Cl Wagsta/T S.S., Jr.: Implementation of the continued fraction inleger factoring algonthm. Proc. J2th Winnipeg Conference on Numerical Methods and Computlng, 1983.

6.    Wunderlicfa M.C.: A running time analysis of Brillharfs continued fraction factoring method. Number Theory, Carbondale 1979, Springer Lecture Notes, 1979, 751, s. 328-342.

7.    Wunderhch M.C.: Im piem en ling the continued fraction factoring algorithm on parallel machi-nes. Math. Comp., 1985, 44, s. 251-260.

5.5. Metoda sita kwadratowego

Metoda sita kwadratowego dla rozkładu na czynniki dużych liczb całkowitych, opracowana na początku lat osiemdziesiątych przez Pomerance’a, przez długi czas była skuteczniejsza od każdej innej ogólnej metody rozkładu, działającej dla dowolnych liczb nie mających dzielników pierwszych rzędu wielkości znacznie mniejszego niż >Jn . (Dla liczb n szczególnej postaci mogą istnieć znacznie szybsze, specjalnie stworzone metody; dla liczb mających dzielnik

pierwszy znacznie mniejszy niż \Jn metoda rozkładu za pomocą krzywych eliptycznych opisana w podrozdziale 6.4 jest szybsza, Porównaj również dyskusję metody sita ciał liczbowych na końcu tego podrozdziału.)

Metoda sita kwadratowego jest odmiana metody baz rozkładu omówionej w podrozdziale 5.3. Jako bazę rozkładu B bierzemy zbiór wszystkich liczb pierwszych pśP (gdzie ograniczenie górne P jest dobrane w pewien optymalny sposób) takich, źe liczba n jest resztą kwadratową modulo p, tzn. że

dla liczb nieparzystych p zachodzi równość (-1=1; liczbęp = 2 zawsze włą-

\ⁿJ

czarny do 5. Zbiór S liczb, wśród których szukamy /Miczb, jest taki sam jak zbiór, którego używaliśmy w metodzie faktoryzacji Fermata (por. podrozdział 5.3), mianowicie

S = {/² - n: [yfn ] + 1 ^ t < [Jn ] -f A}

dla odpowiednio dobranego ograniczenia górnego A.

Główny pomysł, na którym jest oparta ta metoda, polega na tym, by zamiast rozpatrywać po kolei wszystkie je S i dzieląc je przez liczby pierwsze peB, sprawdzać, czy są one ^-liczbami, brać po kolei wszystkie liczby peB i badać podzielność przez p (a także przez potęgi p) jednocześnie wszystkich liczb jeS. Nazwa „sito” odnosi się do tego pomysłu. Przypomnijmy tu „sito Eratostenesa”, za pomocą którego możemy utworzyć listę wszystkich liczb pierwszych p ^ A. Aby na przykład utworzyć listę wszystkich liczb pierwszych nie mniejszych niż 1000, wypisujemy wszystkie liczby całkowite < 1000, a następnie dla każdej liczby p = 2, 3, 5, 7, 11, 13, 17,19, 23, 29, 31 skreślamy z naszej listy wszystkie wielokrotności p większe od p, czyli „przesiewamy liczby przez sito, którego oczka są oddalone od siebie o p” - liczby, które pozostaną, są liczbami pierwszymi.

Naszkicujemy procedurę, za pomocą której możemy zrealizować ten pomysł, a następnie podamy jeden przykład. Ta szczególna wersja procedury, którą tu pokażemy, jest tylko jednym z wielu możliwych jej wariantów i nie musi być wariantem najbardziej efektywnym. Co więcej, nasza przykładowa liczba n, którą będziemy rozkładać na czynniki (a także liczby, które proponujemy rozłożyć na czynniki w ćwiczeniach na końcu tego podrozdziału), jest rzędu «10 ⁶, tak by uniknąć konieczności używania wielkich tablic. Tak mała liczba n jest jednak o wiele za mała, by dobrze ukazać oszczędność czasu płynącą z metody sita przy znajdowaniu dużego zbioru JMiczb.

Przypuśćmy zatem, że mamy daną dużą złożoną liczbę nieparzystą rt.

1. Wybierzmy ograniczenia górne P i A, mniej więcej rzędu wielkości

Na ogół liczba A powinna być większa niż P, ale jednak nie większa niż pewna niska potęga P, np. P < A < P².