56527 skanuj0008

fe^-j - 2 UZ.' -UęJ nu-UX UU W W)Ą /u^J
es2 = 500 + 0,5 • 300-40 = 610 mm (0,61 m). . ^
Sjjjgjaf'’
Ponieważ esl = 390 >0,5 -300-40 = 190 mm, mamy do czynienia z przypadkiem dużego mimośrodu.
A. Obliczenie metodą ogólną
Ze wzoru (5.4) ustalamy wartość momentu
MSdl = 0,180 • (0,50 - 0,5 • 0,30 + 0,04) = 0,0702 MN • m.
a następnie z zależności (5.12) określamy
/W =
0,0702
1,0 0,262-0,85-10,6
= 0,115 = 0,180.
Ponieważ wyznaczona wartość £ odpowiada zakresowi lb, zbrojenie As2 jest obliczeniowo zbędne. Zgodnie z PN-99 zakładamy jednak minimalne pole przekroju tego zbrojenia. Ze wzoru (5.27) otrzymujemy
A,2 min = 0,002 ■ 0,26 • 1,0 = 0,00052 m2 (5,20 cm2).
Z tablicy Z.2 (załącznik) przyjęto w obliczanym przekroju pręty 0 12 mm rozmieszczone co 200 mm ^2.prov = 5,65 cm2 >5,25 cm2.
Ponieważ pole przekroju zbrojenia ściskanego jest większe od zera, należy skorygować zasięg strefy ściskanej. W tym celu wyznaczamy ponownie współczynnik /r (z uwzględnieniem pola przekroju zbrojenia As2 i naprężeń w tym zbrojeniu). I tak, dla:
a-,
0,180, —
d
40
-= 0,154, £
260
210
200000
= 0,00105 (1,05%,),
ze wzoru (3.46) obliczamy
0,300.
0,180-0,154 1
1-0,18 ' 0,00105
Identyczną wartość współczynnika ks2 można po odpowiedniej interpolacji otrzymać z tabl. 3.5. Obliczamy ponownie ze wzoru (5.14)
= 0,102 —>£ = 0,165.
0,0702 - 0,000565 • (0,26 - 0,04) • 0,30 -210
1,0 - 0,262-0,85-10,6 Dla tej wartości £
0,165-0,154
1
- = 0,13.
1-0,18 0,00105
Wobec zmiany naprężeń w zbrojeniu ściskanym należy ponownie skorygować £ 0,0702-0,000565 • (0,26 - 0,04) • 0,13 • 210
1,0-0,262-0,85 -10,6
= 0,110—»£ = 0,175.
«£rU.
, nm o.iis-ą-is9 1
J; £ <f3
kt7 = O,Ol--------— = o 24
A^OJ8 0,00105 ’ ‘
Zatem po kilku krokach iteracji
A =
_ 0,0702 - 0,000565 • (0,26 - 0,04) • 0,244 • 210
1,0 - 0,262 • 0,85 • 10,6
= 0,106—>£ = 0,170.
Ponieważ wartość £ = 0,170 różni się od poprzedniej (£ = 0,175) mniej niż o 5%, tak więc iterację można uznać za zakończoną. Ostatecznie
0,170-0,154
1
1-0,18 0,00105
0,19.
Przyjmujemy jednocześnie z tabl. 3.4 współczynnik a) = 0,115. Teraz obliczamy pole przekroju zbrojenia rozciąganego ze wzoru (5.15)
A | = (0,115 • 1 • 0,26 • 0,85 • 10,6 + 0,000565 • 0,19 • 210 + 0,180) — =
1 210
= 0,002247 m2 (22,47 cm2).
Z tablicy Z.2 przyjęto pręty poziome 0 18 mm rozmieszczone co 110 mm; Asl prov = 23,20 cm2 >22,47 cm2.
B. Obliczenie metodą uproszczoną
W metodzie uproszczonej zakłada się z góry możliwość pełnego wykorzystania efektywnej strefy ściskanej. Dla stali klasy A-I z tabl. 3.9 odczytujemy Ęeff lim = 0,62; przy tym założeniu pole przekroju zbrojenia ściskanego obliczamy ze wzoru (5.24)
AS2 ~
0,180 • 0,39 - 0,62 • (1 - 0,5 • 0,62) • 0,262 • 1,0 • 0,85 • 10,6 (0,26-0,04)-210
=-0,0041 <0.
Wynik ujemny oznacza, że zbrojenie ściskane nie jest potrzebne obliczeniowo. Podobnie jak w metodzie ogólnej zakładamy, że zbrojenie Asl stanowią pręty 012 mm rozmieszczone co 200 mm (minimalny stopień zbrojenia). Rzeczywisty zasięg efektywnej strefy ściskanej lokuje się poniżej wartości granicznej. Przy wyznaczaniu wartości £e// można skorzystać ze wzoru (5.14) i tabl. 3.10.
^// =
0,0702-0,000565 • 210- (0,26 - 0,04) 0,262-1,0 - 0,85-10,6
0,072 -> Ęeff = 0,075.
Warunek (5.22) nie został spełniony, gdyż
£e// = 0,075 <
2-0,04
0,26
0,308,
tak więc zbrojenie rozciągane należy wymiarować ze wzoru (5.26). Otrzymujemy
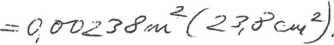
Wyszukiwarka
Podobne podstrony:
skanuj0008 fe^-j - 2 UZ. -UęJ nu-UX UU W W)Ą /u^J es2 = 50
6 uuMJHitfiii i juiniciiiz.ć(t:yjiiy pizez-iitiuzuiiy uu ueiuw wuuKdoyjiiyun, uu uz.yi.NU
skanuj0014 (247) -Mfeututcu ? My t^uiop-id -/uu&fra&. łcbeutypiccky milki C^k^atucą) %dJb(^
komunikowanie6 M fe uC^^CO/C Lr UX^CUXUC kup, ŁpKJO , b^tui) Kmjl^ BlcR l K^^GL
skanuj0044 (6) g 7 - fe - 6W **>e ~ ..~ &nbs
o Cd Nu LUO, I. UU AilOPc lii, AiKIPc UU Od° UlJI,m <idw uu mx u_n, On uu <3Pc on, <pc UU V
skanuj0001 fe-UHgyuftung- $■1 &£*)&y ^ - Hć U«.i~£. /£_ u b.Ta^^t/i VvXvJ*(fc(£)MJ1* 0(f
skanuj0002 (20) rH H. i f§ p i <0- et ŁLct i uU • N r jM -
skanuj0006 (392) I ECH^OLCterA iMWjl w^uX. K f-ilłrO.CjĄ ; O&OU " jL. Uźu. •“ C.$fet£ od
skanuj0015 2 2 Fe * + H2S — 2 Fe2 + §rt + 2 H* Fe3* + e H2S Fc7* S° +2 H + 2e 2 1 Redukcja jonów F
skanuj0029 w. • fe KjjĄf / ,y **■ > . £ J / L i A zabawa taneczna 9 V JAJ »y CD
więcej podobnych podstron