58233 P1050576

2

j||§§

2

cpii

Wprowadzenie

Większość obiektów spotkanych ,_aii równaniem różniczkowym postaci

w liniowych układach automatycznej regulacji

można

a„

d'y{t)

dl”

dr'

-^La₀y(t)=b_m

Ml jI    .₊6₀zr(/j

o'/" ^m_l

J«ali spełnione są następujące warunki: _aj obiekty w układzie sterowania są liniowe, y sygnały podawane są przy zerowych warunkach początkowych, c) sygnały wejściowe spełniają warunki dla istnienia transformaty Laplace a ^    ..

wówczas równanie powyższe, poddane obustronnemu przekształceniu Laplace a przy postać

X a„s”Y(s)+a^ j"¹ Y(s)+...+c₀Y(s)=b_ms^mU(s)+... +b_aU(s) stąd

Y(s) b_m s^m +b_m__ls^m~' + ...+b_ls+b₀

U(s) a_n s"+a_ll__I s”~'+...+as, +a_Q    T

Siosunek transformaty sygnału wyjścia do transformaty wejścia nazywamy transmitancją Operatorową układu i oznaczamy jako G(s)

G(s)=

m

m

7'rausmitancja widmowa

Opis własności układu polega na podaniu zależności pomiędzy sygnałami wyjścia i liścia. W układach liniowych przy podawaniu na wejściu sygnału sinusoidalnego na wyjściu ^r«f awia się także sinusoida o tej samej częstotliwości, ale na ogół o innej amplitudzie i rzesunięta w fazie w stosunku do sinusoidy wejściowej (rys. 1).

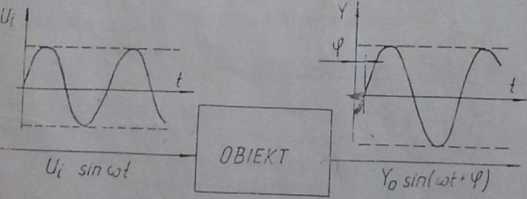
^RVS ' mo_Z^Pr!f²-r^{lt,adU lini0WC80} I wyduszenie sinusoidalne Sygnał wejściowy « ^POpra“ ^dWi° ^Widk0iCI' I il U wyjściowy poprzez Y,