63560 tablice2

■ •    » •• “• • •« ll •• • —•    «>•.(

_W zorij J>£ditaupnę rathanlu__uelclorouego

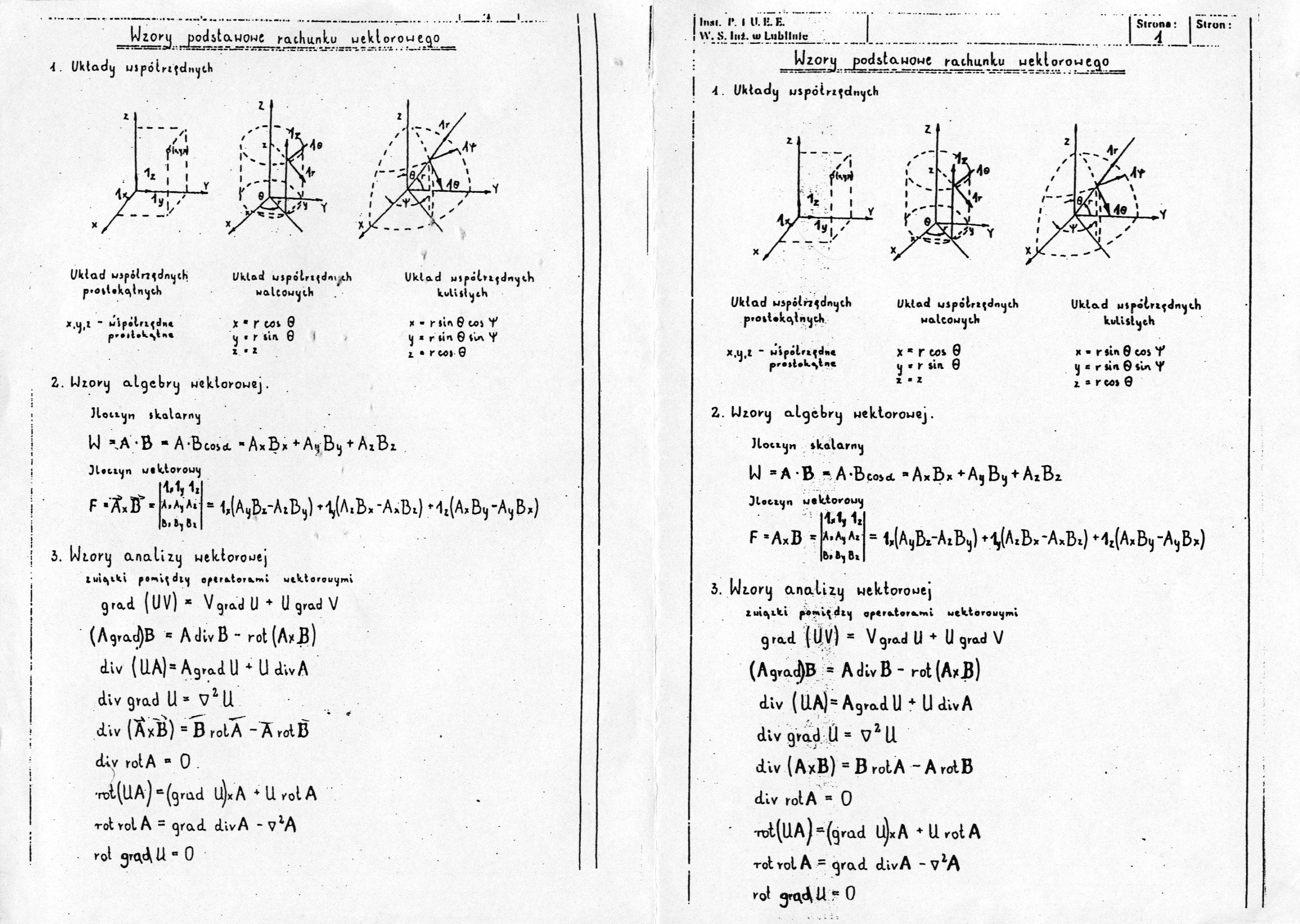
Ą. Uktady uipótrifdnytk

/i

fM

1 '

1

r

'/

l/klad uspćlri{d*i .ch walcou^th

Układ *j*pól*t{dn\j cVt kulili

Układ u3polrx^dmjch ptóiltko^(n<jcK

X,VJ_fl " wlpalnfdnc

X • r COi 0

tj t r iia 0

x • x

* • r lift 0 to* Y

lj * r li n 0 Iwa Y

1 • r coi 0

2. Uzo^y algebry wektorowej.

Jloti\jn skalarny

W "A;B * A-Bcosol -A*Bx ♦AyB^AzBr

Jl.Łlun ułkAoroug

^    1*1j 1ł

F ■/?xfi* ^{r A}'V*

Bi 5^ Bi

~ 1,(A,B»-A»B,)^A.B,-A*B,) M_t(AxEitj'A^Bx)

3. UJLo^y analizy wektorowej

l ulotki p9«iv^di<j eptratorflwmw nikt oranymi

grad (UV) * V grad U ⁺ U grad V

(Ag ra df}B = A div B “ rot (AxB) div (li A) ^s A grad 11 ⁺ U d'wA div grad U * V^2, U d'iv (AxB) ⁼ B rot A "A rotB

d*v rot A " 0 .

\

rol(UAj ^Ł(grad ujxA ⁺ Uroi A rot roi A ⁼ grad divA ~ vV\ rot grąd U ⁰ 0

Itmi. P. I U. K. Ł W. S. Inl. ui Lublinie

Strona: >1

Stron :

kl

Wzory podstawowe rachunku wektorowego

4. Układy współrzędnych

/\

1 ¹ '

\^Z \ '

luj ''

. V

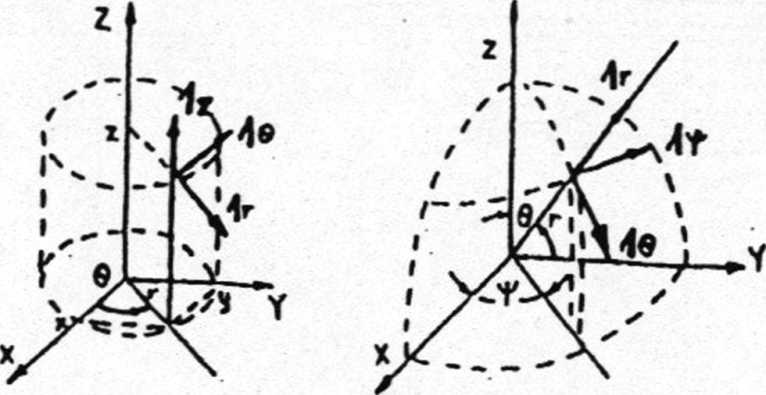
Układ uSpólrtędncjcK MalcOMijck

Układ Mipói n.^dn\j eh kulistych

Układ w5pólri^dnijcK pfO%iakc^łvi<jck

x,u l “ współrzędne pr«)(A^tnt

x * r cos 0 ij * r sin 0 x • z

* • r sin 0 coj Y U « r sin 0 sin Y

z * r cos 9

2. Uzory algebry wektorowej.

Holi yn skalarny

W =A-B “:A-Bco5dL " AxB* + Aj Bij + AlBz

Jloct^n uaktorou^

F ^aAxD

At A) A* B» Bt

⁼ 1>i(Ai_łE>x~ArE>t_J) ♦1_ł(AtBx*AxBi) ^i_Ł(AxBij ”A^Bx)

5. Wzory analizy wektorowej

% * ’• •

Z Ulotki    Qptri^tor^>nl wektorowymi

grad    ~ V grad U ⁴ U grad V

(A, ra J)B ⁵ A dćv B - rot (A* jj) div ( LLA)-A grad II * U div A div grad Ą * V ² U div (AxB) ⁼ B rot A ~ A rotB div rot A ^c 0

(UA) = (grad Ll)xA * U. roi A rot roi A ⁼ grad divA ~ V*A

roi yoA U “ 0