65693 rozdział 9 (15)

i inwestycji uwzględniające wartość pieniądza w ansie 275

A

jpak wydatkiem). Dodatkowo przepływy pieniężne w roku czwar-^pKif o cenę sprzedanych urządzeń (4000 zł).

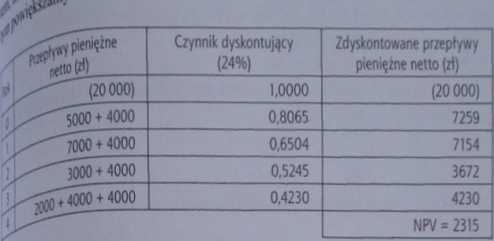
_s 24% projekt należy zaakceptować. Zbadajmy teraz, co stałoby się ||p|gdyby koszt kapitału wynosił nie 24%, ale 36%.

*	pieniężne netto (rł)	Czynnik dyskontujący (36%)	Zdyskontowane przepływy pieniężne netto (zł)
	(20 000)	1	(20000)
	---- 5000 + 4000	0,7353	6618
|7	7000 + 4000	0,5407	5948
h	3000 + 4000	0,3975	2783
	2000 + 4000 + 4000	0,2923	2923
			ŃPV = -1728

fny wzroście kosztu kapitału do 36% inwestycja w nową linię technologiczną aje się nieopłacalna, gdyż generuje u jemną NPV równą NPV=-1728 zł.

Wramach podsumowania należy stwierdzić, że jakość oceny opłacalności in-retycji metodą NP'V zależy od:

I) poprawnego określenia kosztu kapitału (czy to kredytu czy kapitału własnego),

3) prawidłowego szacunku przepływów pieniężnych w przyszłości,

]| wpływu inflacji, która generalnie komplikuje analizę.

3.4. Wewnętrzna stopa zwrotu

Jak zaobserwował iśmy w przykładzie ilustrującym metodę NPV, w zależności odwieikości czynnika dyskontującego (r), NPV projektu może przyjmować różne Miłości-ujemne, i wówczas inwestycja jest nieopłacalna, bądź dodatnie, i wów-fflsprojekt powinien być zrealizowany. W wielu sytuacjach niezwykle istotna jtslkwestia określenia krytycznej wartości stopy zwrotu z realizowanego projek-iu. tj. takiej stopy zwrotu, przy której NPV = 0; będziemy ją nazywać wewnętrzną