67430 P1080234

4. Wprowadzenie do kinematyki robotów

Ograniczenia dotyczą sposobu realizacji ruchu, a konkretnie prędkości, nie zmniejszają jej wymiaru, ale są nieusuwalne. Opisują one, po jakich prostych i krzywych może poruszać się robot, który ma określoną orientację. Ograniczę-nia te są nazywane nieholonomicznymi i dotyczą większości klas robotów mobilnych. Ograniczenia takie modeluje się jako układ, wyprowadzany z analitycznego zapisu ograniczeń ruchu robota.

Zagadnienie kinematyki robotów mobilnych opisano na podstawie pracy [98], na przykładzie układu jezdnego typu samochód. Robot taki może mieć dwa koła tylne o stałych osiach i dwa koła przednie sterowane, o zmiennym kącie ustawienia względem osi robota (rys. 4.24) i jest sztywnym, dwuwymiarowym ciałem poruszającym się w płaskiej przestrzeni roboczej R².

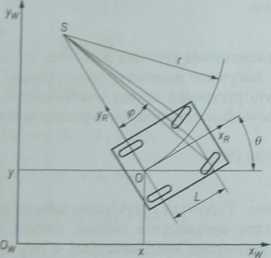
Rysunek 4.24 Jt. \    _

Schemat oznaczeń czterokołowego robota mobilnego typu samochód

Przy założeniu braku poślizgu kinematyka takiego robota jest identyczna jak robota trójkołowego - z jednym kołem sterowanym. Dla większej przejrzystości wzorów w dalszej części pracy będzie wykorzystywany właśnie taki model trójkołowy (rys. 4.25).

Niech punkt charakterystyczny O robota mobilnego będzie tzw. punktem dyferencjału, czyli punktem leżącym pośrodku osi kół tylnych. Niech O_r będzie kartezjańskim układem współrzędnych związanym z robotem A, o środku w punkcie charakterystycznym robota O i osi OX skierowanej wzdłuż jego osi. Każdy punkt pojazdu ma określone swoje położenie w Or. Zmiennymi konfiguracyjnymi tego robota, określającymi jego konfigurację, niech będą współrzędne kartezjańskie jc, y punktu charakterystycznego O robota A w układzie Ow oraz kąt 0 określający orientację robota (kierunek między osiami OX w układach współrzędnych Ow i Or). Przestrzeń konfiguracyjna takiego robota jest równa 114    J?²x(0,2n), a jej wymiar n = 3.

robotów

S

e

y

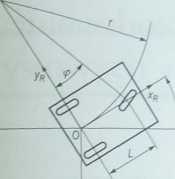
Rysunek 4.25

Schemat oznaczeń trykotowego robota mobilnego typu samochód

Założenie braku poślizgu nakłada na robota pewne ograniczenia. Wiążą się one z tym, że chwilowa prędkość koła w punkcie styku z podłożem jest równa zeru. W związku z tym prędkość chwilowa robota w tym miejscu musi być prostopadła do osi koła. Ponieważ oś dwóch tylnych kół jest prostopadła do osi robota, więc prędkość punktu charakterystycznego O jest równoległa do osi pojazdu. Przyjmując za u prędkość chwilową punktu charakterystycznego 0. można zapisać

(4.80)

(4.81)

x = vcos0, y—v sin#

a po przekształceniu

-isin 9+y cos 6 = 0

Jak można zauważyć, równanie to ma postać równania (4.78) i nie da się go przedstawić w postaci (4.76), czyli opisuje ono nieholonomiczne więzy dwustronne. Idąc dalej tym tokiem rozumowania, łatwo zauważyć, że chwilowy środek obrotu robota znajduje się w punkcie S, na przecięciu osi przedniego i tylnego koła. Stąd po oznaczeniu przez ę kąta skręcenia koła stemjącego oraz przez L odległości między osiami kół, promień skrętu r oblicza się z następującego wzoru

L

tg <P

(4.82)

a krzywiznę K toru ruchu punktu charakterystycznego O ze wzoru

L

(4.83)

115