71762 Slajd5 (107)

Minimalizacja i mapy Karnaugha

Ponieważ dla funkcji logicznych nawet tak prostych jakXOR może istnieć wiele różnych realizacji, często jest pożądane znalezienie najprostszego lub najwygodniejszego w realizacji układu dla danej funkcji. Istnieje wiele dostępnych metod, w tym także algebraicznych, które można zakodować i uruchomić na komputerze. Dla problemów z czterema lub mniejszą liczbą wejść mapa Karnaugha jest jedną z najsympatyczniejszych metod: pozwala przy tym napisać wyrażenie logiczne (jeżeli go jeszcze nie znasz) prawie bezpośrednio z tablicy prawdy.

Przykład. Załóżmy, że chcemy zaprojektować układ zliczający głosy. W yobraź sobie, że masz trzy wejścia w logice dodatniej (każde w stanie 1 lub 0) i jedno wyjście (w stanie 0 lub 1). W yjście ma wykazywać jedynkę, jeżeli co najmniej na dwóch wejściach są jedynki.

A	H	c	Q
0	0	0	0
0	0	1 %	c
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	a	1
l	1	i	1

Krok 1. Napisz tablicę prawdy:

Musisz w niej zapisać wszystkie możliwe permutacje wejść wraz z odpowiadającymi im stanami wyjścia. Napisz X (= "dowolny"). jeżeli każdy stan jest dobry.

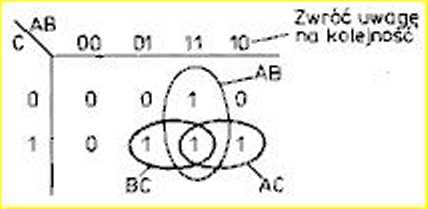
Krok 2. Zrób z tego mapę Karnaugha. Jest ona trochę podobna do tablicy praw dy, ale zmienne są rozmieszczone w dwóch osiach. Co więcej, są poprzestawiane w taki sposób, że przy przechodzeniu między sąsiednimi kratkami zmienia się tylko jeden bit wejściowy