72186 skanuj0034 (42)

	Naturalny kod dwójkowy				Kod Graya			a
	b3 b2		B1	Bo	g3 g2	Go	G4
0	0	0	0	0	0 0	0	0
1	0	0	0	1	0 0	0	1
2	0	0	1	0	0 0	1	1
3	0	0	1	1	0 0	1	0
4	0	1	0	0	0 1	1	0
5	0	1	0	1	0 1	1	1
6	0	1	1	0	0 1	0	1
7	0	1	1	1	0 1	0	0	Oś
8	1	0	0	T	1 1	0	0	symetri
9	1	0	0	1	1 1	0	1
W	1	0	1	0	1 1	1	1
11	1	0	1	1	1 1	1	0
12	1	1	0	0	1 0	1	0
13	1	1	0	1	1 0	1	1
14	1	1	1	a	1 0	0	1
15	1	1	1	1	1 0	0	0

Kod Graya

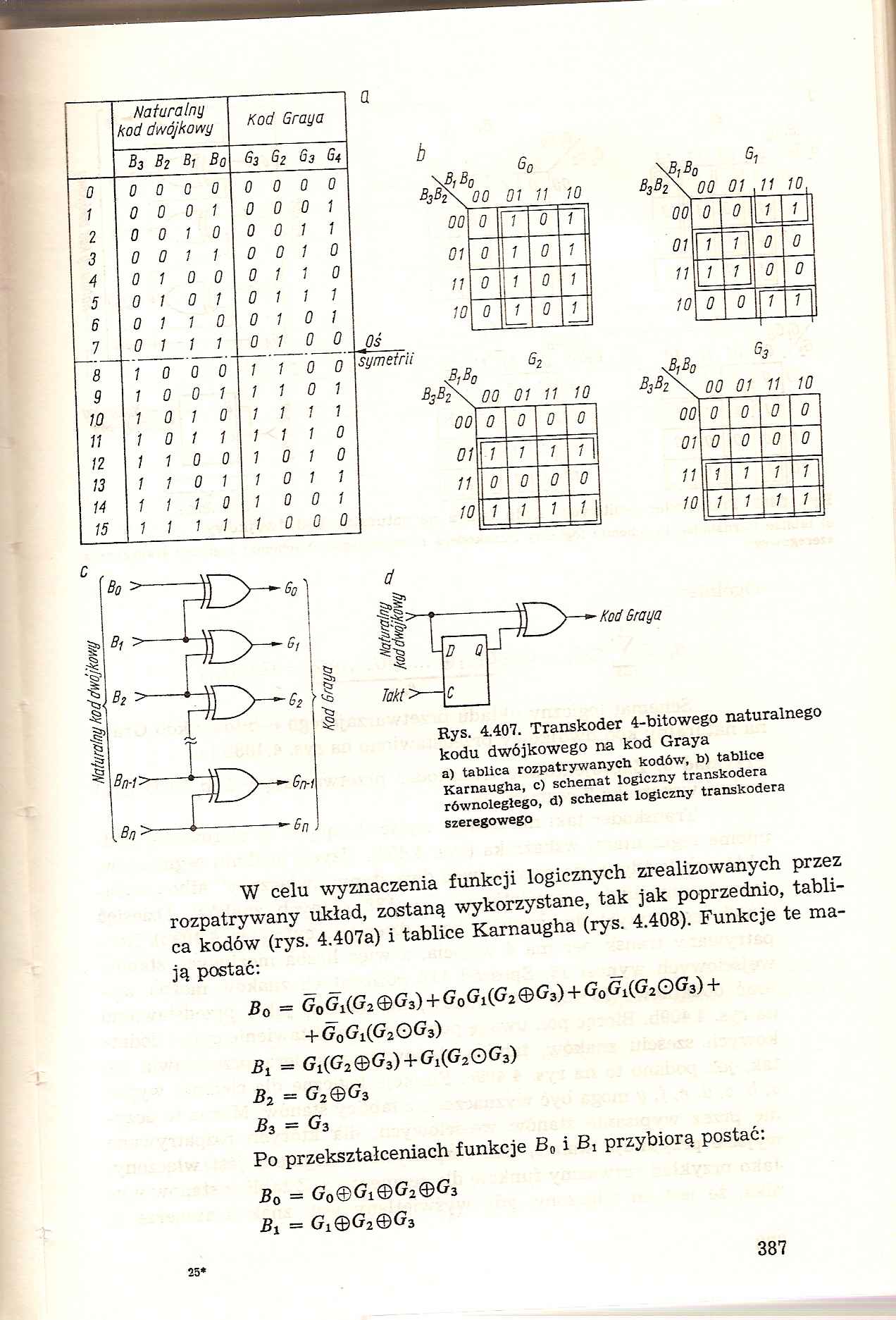
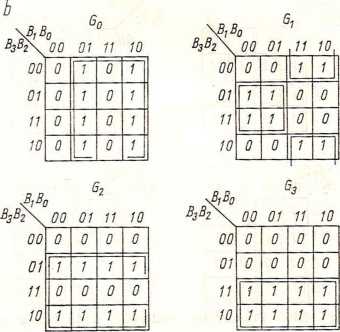
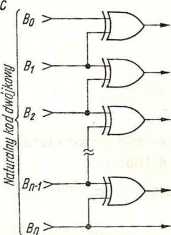
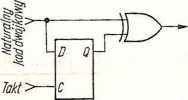
Rys. 4.407. Transkoder 4-bitowego naturalnego kodu dwójkowego na kod Graya

a) tablica rozpatrywanych kodów, b) tablice Karnaugha, c) schemat logiczny transkodera równoległego, d) schemat logiczny transkodera szeregowego

W celu wyznaczenia funkcji logicznych zrealizowanych przez rozpatrywany układ, zostaną wykorzystane, tak jak poprzednio, tablica kodów (rys. 4.407a) i tablice Karnaugha (rys. 4.408). Funkcje te mają postać:

Bo = G₀G₁(G₂®G₃) + G₀G₁(G₂®G₃) + G₀G_i(G₂®G₃) +

+G₀G_x{G₂OGs)

Bi = Gi(G₂@G₃) + G₁(G₂QG₃)

B₂ = g₂@g₃ b₃ = g₃

Po przekształceniach funkcje B₀ i B₁ przybiorą postać:

B₀ = G₀®G₁@G₂®G₃ B_x = G₁®G₂@G₃

25*

387