72688 skanuj0008 (323)

Schemat statyczny

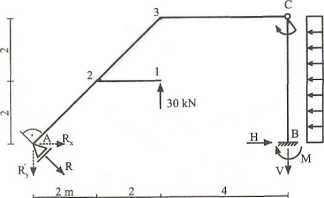
Wobec zachowanego kryterium ilościowego jest on statycznie wyznaczalny. Ponieważ tarcza BC ma odebrane wszystkie stopnie swobody to można ją utożsamić z ostoją, do której dołączono tarczę AC. Schemat ustroju ma wyraźnie charakter hierarchiczny; z tarczą podstawową BC, tarczą podrzędną AC (podukład). Można zatem rozwiązywać układ w sposób pośredni, tzn. w pierwszej kolejności rozwiązać w pełnym zakresie tarczę podrzędną AC, a następnie wyznaczonymi reakcjami (z przeciwnymi zwrotami) obciążyć w punkcie C tarczę CB. Dla układu jako całości są to interakcje (w tym przypadku siły przekrojowe). Wersję rozwiązania pośredniego przedstawia się poniżej, po rozbiciu na podukłady.

Tarcza A-C

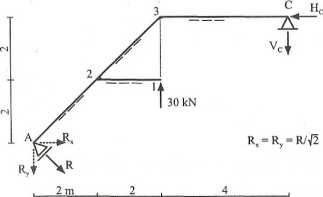
Reakcje

XM_iC = 0, —J?_x* 4—.R_y* 8 + 30*4 = 0,

R_x = R_y=+10 kN, i? = 10^2 kN,

IP_U = 0, R_x-H_c = 0, H_C = R_C= +10 kN,

ZP_ly - 0,    -R_y+30-F_c = 0, V_c — 30—■» +20 kN.

a._

Siły wewnętrzne wyznaczamy w przekrojach charakterystycznych. Siły osiowe

n₁₂ = o = n₂₁, n_A2 = o=n_2A,

N₂₃ = -30-0/2 = -150 kN = N₃₂,

N_C3 m -H_c = -10 kN = N_3C.

Siły tnące

r₁₂ = - 30 kN = T₂₁, T_a1=-R mm 100 kN = T_2A,

T₂₃ = 7^+300/2 = -100+150 = +50 kN = T₃₂, r_CB= +V_C= +20 kN = T_3c.

Momenty gnące

0,    M₂₁ = +30-2 = +60 kNm, M_A = 0,

M_2A = -R-2y/l= -l0y/2-2y/2= -40 kNm,

M₂₃ = -£• 2^2- 30-2= -40 - 60= -100 kNm,

M₃= -i?-4V^= -10-_v/2-4>/2= -80 kNm = -F_c-4 = -20*4 = = -80 kNm.

Tarcza C-B

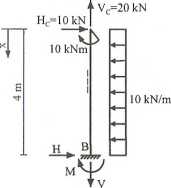
Wyznaczenie reakcji (w tym przypadku nie są one potrzebne do obliczenia sił przekrojowych)

ZX = 0,    10-4- 10+tf = 0, H = + 30 kN,

ZT = 0,    20-F = 0, F = +20 kN,

ZM_b = 0, M+10+10-4—10-4-2 = 0,

M = +30 kNm.

Siły przekrojowe przedstawia się funkcyjnie dla xe(0; 4 m)

N{x) = + V_c = 20 kN = constans = + F,

T(x) = H_c— 10x = 10- 10x,    T{0) = 0, T(4) = -30 kN = — H,

Af(x)= +10+H_c-x—10-x--x = 10+10x—5x²,

M(0) = +10 kNm, M(4) = -30 kNm = dM

ekstremum M -* —— = = 10— 10x = T(x) = 0 -> x = 1 m, dx

M(l) = 10+10—5*l² — +15 kNm, miejsce zerowe M -*• M — 0-» 10+10x—5x² = 0 -► x²—2x—2 = 0 x - 2,732 m x--0,732 m.