69620 PB032239

rozbieżnych jeden jest rozbieżny.

O ciągach mających granice niewłaściwe mówiim, lub -oo.    ^lmy’ że _Są

Niżej podajemy kilka twierdzeń dotyczących d ńeżnych oraz działań arytmetycznych na ciąg^^^

Twierdzenie 6.15. Dla każdego a > l .*

_Tilim_jaⁿ = ₊oo.

Twierdzenie 6.16. Dla każdego a > 1;

lim n^Q = +oo.

n—»oo

Twierdzenie 6.17. Jeżeli    = +oo (lub -oo) to-

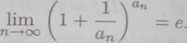
Twierdzenie 6.18. Jeżeli lim a_n = a i lim b_n = +oo to-

n—* oo    n—»oo    ’

1° lim (a„ -f 6n) = +oo, n—*oo
2° lim (a„ • 6„) = < n—»oo . 1 —OO,	gdy 9dy	a > 0, a < 0,
lim fc = 0, przy 6n 7^ 0 d/a n G N, ^n~*°° bn
4° lim ± 1 1 +°°’ n-*oo an [ —oo, gdy	a > 0, a < 0,	przy założeniu że an "

• * >00, ^

Twierdzenie 6.19. Jeżeli lim Q>n ⁼ +°° * _nlHJx> >

n—»oo

lim (a_n + b_n) = +oo,

n—»oo

2° lim (a_n - b_n) — +oo.

Tl—* OO