69625 P1160474

Ilość przesączu otrzymana z lm³ powierzchni filtrującej wynosi:

V- + 2C₂-V=K₂ T

V + 2-V I.63-10”³ =1,914-10"⁶-1800

po rozwiązaniu równania kwadratowego otrzymuje się:

V = 0,067 m³ = 67 litrów przesączu

Przykład 26

Czas filtracji 20 m³ zawiesiny wodnej wynosi 2,5 godz. Określić orientacyjnie czas przemywania osadu przy użyciu 2 inl wody przyjmując, źc szybkość przemywania jest czterokrotnie mniejsza od szybkości filtracji w końcowym jej momencie. Opór tkaniny filtracyjnej pominąć.

Dane:

V = 20 m³

t«25h

V.=2n»^J

Rozwiązanie:

Równanie filtracji w warunkach, gdy pomija się opór tkaniny filtracyjnej (0=0) ma

postać:

V² = k T

Stała szybkości filtracji dla tego przypadku wynosi:

T

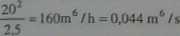
Szybkość filtracji:

Szybkość przemywania jest czterokrotnie mniejsza od szybkości fikracji (z załozrmar

(—)przemywania = 1,1 -10"³:4«2,75-10"⁴m³/s = (^”)p dit    ot

Czas przemywania wynosi zatem:

7272 s

V, 2 ^T” ⁼ ^jp 2,7510-*

Przykład 27    |

Ściana budynku inwentarskiego o grubości 0,25 m wykonana z cegły o współczynniku przewodzenia ciepła równym 0,814 W/(mK), ocieplona została od zewnątrz warstwą wykonaną z płyt wiórowo-cementowych (suprema) o grubości 0,05 m i współczynniku przewodzenia ciepła równym 0,093 W/mK. Obliczyć przy jakiej temperaturze zewnętrznej powierzchni ściany na jej powierzchni wewnętrznej pojawi się szron. Straty ciepła z I m² powierzchni ściany wynoszą 20 W/m². Obliczenia wykonać dla ściany bez izolacji i dla ściany ocieplonej warstwą supremy.

Dane:

S| = 0,25 iii X, =0,814 W/mK A = 1 m² «2 = 0,05 m X₂ -0,093 W/mK Q - 20 W / m¹

Rozwiązanie:

Szron pojawi się na wewnętrznej powierzchni ściany, jeśli jej temperatura oo«i*> się do 0 °C.

Strumień ciepła przewodzonego przez jednowarstwową ścianę płaską oblicza się następująco, (wzór (4.2)):

Q““^A(t| -l₂)

Temperaturę zewnętrznej powierzchni ściany jednowarstwowej tj oblicza s*ę aaMę-pująco:

-6.1 *C

iL.o-20-^

■aJx,    0,814

87