74667 PICT0085 (4)

Wa płaskiego stanu napięcia przy *₃ •= 0 równanie plastyczności Hubera przedstawia ełćpsę (rys. 9) będącą śladem przecięcia walca Hubera jkzez płaszczyznę —a₂. Klipsa ta jest opisana na sztściokącie przedstawionym na rys- 7. Wspólne punkty elipsy i sześciokąta przedstawiają stany napięcia, dla których obie hipotezy dają zgodne wyniki.

Z równania plastyczności Hubera wynika, że naprężenie zastępcze o_H ma wartość

°B=~- Wl    + (*2 - ”t)³ *    (24)

Naprężenie stycaie na płaszczyźnie ośmiościanu wyraża wzór

=Ą~ V»l ~ «2>² + (°2 ~°3>- + (f₃ - O,)²    (25)

stąd zaś otrzymuje się, że

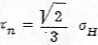
co pozwala równaniu plastyczności Hubera nadać jeszcze jeden sens fizyczny a mianowicie: miarą wytężenia materiału na granicy plastyczności jest wartość naprężenia tnącego w płaszczyźnie ośmiościanu, które w chwili przejścia materiału w stan plastyczny osiąga stałą wartość, określoną dla danego materiału 'i danych warunków obciążenia. • ^r

Chcąc ocenić słuszność obu wymienionych hipotez należy przede wszystkim zwrócić uwagę, że hipoteza największego naprężenia tnącego pomija zupełnie wpływ średniego naprężenia na wytężenie materiału.

Porównanie zgodności hipotezy największego naprężenia tnącego i energii odkształcenia postaciowego z doświadczeniem^ wykazało stanowczą przewagę hipotezy ostatniej, tj. Hubera.