78477 img355 (8)

1.    Zestawić czynności krytyczne, podać ich gradienty kosztów S oraz czasy graniczne t_gr.

2.    Wyeliminować z zestawienia te czynności krytyczne, dla których średni gradient kosztów nie istnieje, tzn. t_n = l_gr.

3.    Proces skracania rozpocząć od czynności krytycznej o najniższym gradiencie kosztów S.

4.    Przy skracaniu czasu trwania czynności należy starać się skrócić jej czas o jak największą liczbę jednostek czasu (dni). Występują tu dwa ograniczenia:

a)    czas graniczny danej czynności t_gr,

b)    pojawienie się nowej ścieżki krytycznej (nowa ścieżka krytyczna pojawi się, jeżeli zaniknie zapas czasu w ciągu czynności niekrytycznych).

5.    Przy istnieniu dwóch lub więcej ścieżek krytycznych w sieci należy skracać czas o tę samą wielkość na wszystkich równoległych ścieżkach krytycznych.

6.    Najkrótszy termin wykonania programu sieciowego uzyskuje się, gdy wszystkie czynności leżące na którejkolwiek drodze krytycznej osiągną czasy graniczne t_gr Dalsze skracanie czasu wykonania programu jest wówczas niemożliwe.

7.    Koszty przyspieszenia oblicza się mnożąc liczbę jednostek czasu (dni), o które dana czynność krytyczna została skrócona, przez jej gradient kosztów.

Zaprezentowany algorytm wyznaczania optymalnego programu akceleracji czynności i określenia najkrótszego czasu wykonania całego przedsięwzięcia przy minimum kosztów stosuje się zarówno do sieci CPM, jak i PERT.

5.5. CPM-COST

Przykład 32. Mając dane charakteryzujące przedsięwzięcie P (tabl. 154) dokonać skrócenia całkowitego czasu wykonania programu tak, aby koszt przyspieszenia terminu ukończenia przedsięwzięcia był jak najmniejszy.

Tablica 154

H	K	*gr		K	S
1-2	8	6	280	400	60
1-1	10	5	100	150	10
2-3	6	4	300	400	50
3-6	12	10	260	300	20
4-5	15	15	150	150	-
5-6	10	2	200	360	20
			1290	1780

Po wykreśleniu siatki zależności (rys. 18) wyznaczamy ścieżkę krytyczną, która przebiega przez zdarzenia 1 - 4 - 5 - 6.

Termin wykonania przedsięwzięcia wynosi 35 dni, a zapas czasu ciągu czynności niekrytycznych 1-2-3-6 wynosi 9 dni. Skrócenie czasu całkowitego wykonania programu można uzyskać dzięki skróceniu czasów trwania czynności krytycznych.

Rozpoczynamy od czynności o najmniejszym współczynniku wzrostu kosztów S, a więc od czynności 1 -4, S = 10. Czas trwania tej czynności możemy skrócić do 5 dni (f_gr=5 dni). Tym samym czas wykonania całego przedsięwzięcia zostanie skrócony do 30 dni, a wzrost kosztów spowodowany tym skróceniem wyniesie

= S At = 10 ■ 5 = 50 jedn. p.

Czynnością, która znajduje się na ścieżce krytycznej, a której czas wykonania może jeszcze ulec przyspieszeniu, jest czynność 5-6. Możliwe jest jednak skrócenie czasu jej wykonania tylko do 6 dni ( o 4 dni), bo ogranicza nas całkowity zapas czasu ciągu czynności 1-2-3-6, który wynosi obecnie 4 dni. W rezultacie termin ukończenia ostatniego zdarzenia wyniesie 26 dni, a koszty wzrosną o K₂ = 4 • 20 = 80 jedn. p.

W tej sytuacji powstaną dwie ścieżki krytyczne:

1 - 2 - 3 - 6

oraz

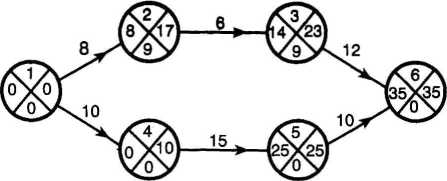
Rys. 18

1 - 4 - 5 - 6.

Możemy jednak w dalszym ciągu dokonywać skracania czasu wykonania programu, bo na obu ścieżkach krytycznych znajdują się jeszcze czynności, które nie osiągnęły czasów granicznych. Można by skrócić czas czynności 5-6 jeszcze o 4 dni, aż do osiągnięcia czasu granicznego 2 dni. Równocześnie należy skrócić czas wykonania czynności 3-6 (o 2 dni) i 2-3 (o 2 dni), leżących na drugiej ścieżce krytycznej (o kolejności skracania czasu czynności decyduje niższy gradient kosztów).

Czas ukończenia przedsięwzięcia będzie zredukowany do 22 dni, a koszty związane ze skróceniem czasu wyniosą:

Czynności Koszty przyspieszenia

/

5-6

3-6

2-3

4-20= 80 2-20= 40 2- 50 = 100 K₃ = 220

167