83577 skanuj0022 (136)

Jako układ zmodyfikowany przyjęto Nchnnmi. w M 6 ryj u niewiadomymi są reakcje oraz siła w pręcie D₂ kratownicy. Równaniu równowagi dla schematu mają postać (wersja klasyczna).

ZX — O_t R.2_X-t-R$_x-ł-P 2 — 0,

gdzie

R_2x — R2y ⁼    P$x ⁼ P$y — P3/V^*

Suma rzutów na oś £

gdzie

2^ = 0,    F_u+F₄*-P_1?-P₂₄ = 0,

V_u = VJy/i, v_t( = mM -Pu = ^pi/\/2. ^p2t = Pi/yfe-Suma momentów względem bieguna 0

IM₀ = 0    F_x -8 +R_zy-2-P_t -4—P₂*4 = 0.

Siłę w pręcie D₂ wyznaczamy metodą przekrojów.

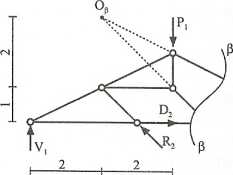
Przekrój a—a

Suma momentów względem bieguna 0a V_ł-2-D₂-1 = 0.

Przekrój fi—fi

Suma momentów względem bieguna 0/? F₁-2+P_2;c-2-2)₂-3+P₁-2 = 0.

Układ równań w zapluta uwuitar/owym ma postać

0 \/<Jl 1 Isfl 0 0 *		’ V		p2
iA/2 o o ify/i o		r2		-PJ^l-PJ+J2
o o 0 1 oo		Rs	+	— 4Pl—4P2
2 0 0 0 -1		v4		0
2 2/y/l 0 0 -3.		d2.		2Pi

Postać zblokowana zapisu macierzowego prowadzi do równania

A-N+P = Ó,

gdzie:

A — macierz współczynników przy niewiadomych,

N — wektor niewiadomyh,

P — wektor wyrazów wolnych.

Niewiadome wyznaczamy z relacji

Ń= -i"¹?.

Macierz odwrotna A"¹ istnieje wtedy, gdy wyznacznik macierzy A jest różny od zera (det A # 0), co jest kryterium analitycznym geometrycznej niezmienności układu.

Analiza wyznacznika układu:

Z rozwinięcia 3-ciej kolumny mamy

	'i/0	0	WS	0
= 1/0	8 2/<y/2 2 0		0 0	0 -1
	2 2/0		0	-3
		'8	2/V2	0 '
		2	0	-1 ,
		,2	2A/2	-3.
		8	2/^2	0 ‘
A% = 1/0	•1/0^1	0	0	-1
		—4	2/V2	-3.

det^ = dcti4₂ - ■^•4-(16_n/2+8>/2) » ^*24^/2 « 12>/2 ^ 0.

63