scan 4

Teraz zobaczymy jak wygląda prawa strona równości. Trzeba w miejsce n do wzoru danego w temacie zadania wstawić n + 1.

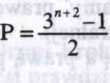
L = P

zatem

Wzór z zadania przekształcamy tak:

n+1

3"⁺¹-l    3"^+l+l-1    3"⁺²-l

Zad.3

Udowodnij, że /\ 4 + 10 + 16 + ... + (6n - 2) = n (3n + 1)

W € N

Dowód:

Pierwszy krok indukcyjny (Sprawdzamy prawdziwość twierdzenia dla początkowej liczby naturalnej). Oznaczamy lewą stronę równania przez L, a prawą stronę przez P.

Niech n = 1, wtedy

L = 4    bo jeśli w miejsce n do

li    6/i-2 wstawimy n = 1, wtedy

61-2=6-2=4

P = «(3*/i +1) = 1 • (3 • 1 + 1) = 1 • (4) = 4

czyli

L = P

Drugi krok indukcyjny (Sprawdzamy, czy jeśli równość jest prawdziwa dla n, to czy też jest prawdziwa dla następnej liczby naturalnej, czyli n + 1).

L-4 + 10 + 16 + ... + (6n — 2) + (6 (n + 1)- 2) —

= n (3n + 1) + (6 (n + 1) - 2) = = /z(3/i + l) + 6(/i + l)-2 =

= 3n ² + /2 + 6/i + 6- 2 =

= 3/2² + 7/z + 4

Tworzymy sumę dla następnego n, wstawiając w miejsce n n + 1, czyli znajdujemy sumę n + 1 wyrazów.

Teraz redukuję wyrazy podobne.

Teraz prawa strona.

W miejsce n po prawej stronie wstawiamy n + 1, czyli

P = (n +1) (3 (n +1) + 1) = = (« +1) (3n + 3 +1) =

= (« + l) (3n + 4) =

= 3n² + 4n + 3rt + 4 =

w+1 n+l

V V

n (3n+ 1)

przekształcamy wyrażenie, mnożąc, redukując wyraży podobne.

= 3m²+ 7« + 4

zatem

L = P

Zad.4.

Udowodnij, że

A _{+    +    +}    _I_=    ”

„_eN 2 5    5-8    8 11    (3«-l)(3n+2)    2(3n+2)

Dowód:

Pierwszy krok indukcyjny (Sprawdzamy prawdziwość twierdzenia dla początkowej liczby naturalnej).

Oznaczamy lewą stronę równania przez L, a prawą przez P.

Niech n = 1, wtedy    W miejsce n we wzorze

(3«-l)(3n + 2)

¹    wstawiamy 1

L =

1 _ 1

(3 • 1—1) (3 - l-t-2)    (3-l)(3+2)    2 5    10

1

1

P =

_ 1 _ 1

2(3 1+2)    2-5    10

1

L = P

13