HPIM5185

Ponieważ skoki wszystkich linii zęba są jednakowe na wszystkich walcach, zatem prawa strona równości (3.88) jest stałą niezależną od promienia walca. Przyjmując za r_v kolejno promienie walca podziałowego r. zasadniczego /■*, i wierzchołkowego otrzymujemy ostatecznie

(3.89)

^r __ ^rb _ ^ra tgP    tg Pb    tgpa

3.2.2.3. Zastępcza liczba zębów

W pewnych zagadnieniach występujących w walcowych kołach śrubowych (również w kołach stożkowych) celowe jest zastąpienie tych kół kołami walcowymi o zębach prostych - równoważnymi pod pewnym względem kołom o zębach śrubowych. Takie równoważne koła walcowe o zębach prostych nazywamy kolami zastępczymi, a liczbę zębów tych kół o module równym modułowi nominalnemu (normalnemu) kół śrubowych (lub stożkowych) nazywamy zastępczą liczbą zębów. Pojęcie kół zastępczych jest użyteczne np. przy formułowaniu warunku nie-podcinania zębów; również w wielu stosowanych obecnie metodach obliczeń wytrzymałościowych koła zastępcze są podstawą budowy modeli wytrzymałościowych, które są oparte na hipotezie, że koła zastępcze są równoważne wytrzymałościowo kołom rzeczywistym.

Przejdziemy teraz do ściślejszego zdefiniowania zastępczej liczby zębów dla kół śrubowych.

Koło zębate o zębach śrubowych przecinamy płaszczyzną normalną N-N do linii zęba na walcu podziałowym (rys. 3.26a). Rozpatrujemy walec podziałowy o średnicy d. W płaszczyźnie N-N przekrój tego walca jest elipsą. Największy promień krzywizny tej elipsy jest promieniem okręgu ściśle stycznego do niej w punkcie C (rys. 3.26d); nazywamy go zastępczym okręgiem podziałowym. Wyznaczymy teraz liczbę zębów prostych, którą można zmieścić na zastępczym okręgu podziałowym o promieniu równym r_asl. Tę liczbę zębów nazywamy zastępczą liczbą zębów. Z podanego określenia wynika, że wyznaczenie zastępczej liczby zębów sprowadza się do obliczenia maksymalnego promienia krzywizny elipsy otrzymanej w opisany sposób.

Z rysunku 3.26a wynika, że półosie elipsy wynoszą

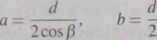
(3.90)

gdzie: a - duża półoś, b - mała półoś.

Największy promień krzywizny elipsy

(3.91)

Jeśli uwzględnimy wzory (3.90), co otrzymamy d    zm

(3.92)

"" “ 2 cos²/? “ 2ćos*jS

Liczba zębów z_v o module normalnym, którą można zmieścić na obwodzie okręgu o promieniu r_asl, jest równa ilorazowi obwodu tego okręgu i podziałki normalnej

(3.93)

2nrzaat

Ze wzorów (3.92) i (3.93) otrzymujemy ostatecznie

(3.94)

cos³/3

W literaturze można spotkać wzór na zastępczą liczbę zębów w postaci

(3.95)

COS² Pt, cos f)

gdzie pf, - kąt linii zęba na walcu zasadniczym.

Wzór (3.95) otrzymuje się wtedy, gdy płaszczyzna N-N jest prostopadła do linii zęba na walcu zasadniczym. Różnica między wzorami (3.94) i (3.95) nie ma jednak praktycznego znaczenia, ponieważ wyniki otrzymane z obu wzorów są sobie bliskie.

3.2.2.4. Graniczna liczba zębów w kołach śrubowych

Podcięcie zębów w kołach walcowych o zębach śrubowych nie występuje wtedy, gdy zastępcza liczba zębów jest większa lub równa granicznej liczbie zębów kół o zębach prostych. Warunek niepodcinania zębów śrubowych ma więc postać

*v>*g    (3.96)

gdzie z_K jest określone wzorem (3.60).

Ze wzorów (3.60) i (3.94) otrzymujemy

cos³#    (3.97)

sur a

Prawą stronę nierówności można nazwać graniczną liczbą zębów w kołach śrubowych. Oznaczając ją przez z_gp, mamy

= ²⁽^r.-"jcos*0    (3.98)

sura

gdzie x„ jest współczynnikiem przesunięcia zarysu odniesionym do przekroju normalnego; omówiony on będzie w następnym punkcie.

Widać stąd, że graniczna liczba zębów koła walcowego o zębach śrubowych z_gp jest mniejsza niż graniczna liczba zębów z„ koła walcowego o zębach prostych.

273