225 (4)

225

warstw, wartość €_rain(k) powinna maleć. Typowy przebieg e_niin(&) przedstawiony jest na rys. 10.9.

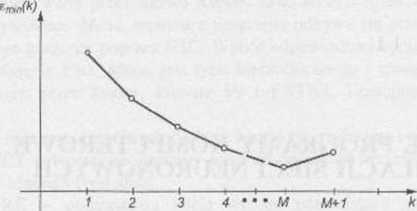
Rys. 10.9. Przebieg wartości błędu w funkcji ilości warstw sieci

Po przekroczeniu pewnej wartości k = M wartość t_min(k) zamiast maleć, zaczyna rosnąć. Oznacza to, że dodanie następnych warstw sieci jest bezcelowe, gdyż nie prowadzi do zmniejszania błędu. Przyjmuje się liczbę warstw równą M, u ostatnia M-ta warstwa staje się warstwą wyjściową. Jedynym neuronem, jaki pozostawiamy w tej warstwie, jest neuron najlepiej wyirenowany. Pozostałe ulegają redukcji. Po zredukowaniu liczby neuronów w ostatniej warstwie należy przeprowadzić redukcję (odrzucenie) tych neuronów w kolejnych warstwach poprzedzających, które znajdowały się na drodze zasilania neuronów zredukowanych, a nie miały innych połączeń z pozostałymi neuronami w sieci. W ten sposób następuje dodatkowa redukcja neuronów w poszczególnych warstwach, po przeprowadzeniu której struktura sieci staje się ostatecznie zdefiniowana. Przy założeniu M warstw sieci funkcja odwzorowująca wektor X w odpowiedź y neuronu warstwy M-tej przyjmuje postać wielomianu stopnia 2M względem elementów wektora wejściowego X. Stąd pochodzi nazwa sieci wielomianowej.

Często w ostatnim etapie projektowaniu sieci wielomianowej stosuje się dodatkowe douczenie ostatecznej struktury sieci, powtarzając proces rozwiązania (10.16) dla kolejnych warstw sieci, przy ustalonej z góry' zarówno liczbie warstw, jak i neuronów w warstwie.

Podsumowując należy stwierdzić, że sieci neuronowe wielomianowe stanowią praktyczną realizację idei poszukiwania doskonałości odwzorowania każdego neuronu w każdej warstwie. Każda nowa warstwa zmniejsza błąd odwzorowania aż do osiągnięcia jego minimum w ostatniej warstwie.

W praktycznych implementacjach liczba warstw może sięgać nawet kilkunastu, realizując aproksymację danych d - yłX) przy użyciu funkcji wielomianowej wielu zmiennych wysokiego rzędu. Nieliniowość wprowadzana przez poszczególne neurony jest typu wielomianowego o dużej gładkości, W związku z powyższym, sieci lego typu dobrze nadają się cło odwzorowania funkcji wielu zmiennych typu ciągłego i wszelkich procesów', które mogą być opisane tego typu charakterystyką.