Wa&St Hydr20
W \l ii i nulu |i f(<5) przedstawiony jest na rys. 6-60, a wartości liczbowe W lnlielcc
ń 20” 40° 60° 80° 90° 100° 110° 120° 130°
0,046 0,139 0,364 0,740 0,984 1,26 1,56 1,86 2,16
W.iitii.ii uzyskane przez Weisbaclia są prawdopodobnie za małe, ponieważ iitiiiic, l inienia określał on niedostatecznie daleko przed i za odcinkiem po-iiiuii iiwytu i stąd też nie uchwycił całkowicie strat przy wlocie i wylocie w prostym odcinku przewodu. Wzór Gibsona
C = 67,6 • 10-6 • ó2>17 [6-64]
daje użytkowe wartości dla technicznie gładkich załamań. Wartości liczbowe obliczone wg wzoru Gibsona zawiera poniższa tabelka, natomiast graficznie zostały przedstawione na rys. 6-60
ó 20° 40° 60° 80° 90° 100° 110° 120° 130°
C 0,043 0,202 0,488 0,911 1,18 1,48 1,82 2,20 2,61
|
2/ /1 | ||
0 50 100 150
ó°
Rys. 6-60. Zależność pomiędzy współczynnikiem o-poru C i kątem S dla załamań
1 — wg Wcisbacha, 2 — wg Gibsona

Rys. 6-61. Współczynnik oporu f dla załamania o kąt 5 = 90° dla zwykłych rur stalowych (D = 50 mm) w funkcji Re
I )ln Ą — 45° wartość f wg Gibsona jest większa o 40% niż wg Weisbacha. Przy <) 90" o 20%, przy <5 = 120° o 18%, co potwierdzone zostało przez badania
przeprowadzone przez innych badaczy.
y.immermann ustalił na podstawie badań zależność pomiędzy współczynnikiem oporu £ i liczbą Re przy przepływie przez załamanie pod kątem prostym dla rury o /) 50 mm (rys. 6-61). Przebieg tej zależności jest taki jak dla kolanka, tyle
tylko, że C posiada wyższe wartości. Poczynając od Re — 600 000, £ = const.
6.11.2. Zmiana przekrojów poprzecznych
Gwałtowne rozszerzenia. Przy gwałtownym rozszerzeniu przekroju (rys. 6-62) występują straty energii strumienia, które możemy określić za pomocą zasady
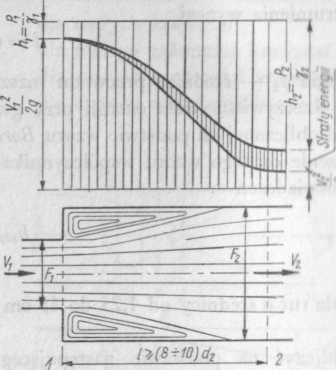
Rys. 6-62. Przemiany energii przy gwałtownym rozszerzeniu przekroju poprzecznego
ilości ruchu. Wydzielimy w tym celu myślowo obszar zawarty pomiędzy płaszczyznami 1-1 i 2-2. Na powierzchnię (F2—F^) działa, jak wiadomo na podstawie doświadczenia, takie samo ciśnienie jak w przekroju Fv Spowodowane jest to tym, że w miejscu rozszerzenia przewodu następuje oderwanie strumienia.
Stosując zasadę przyrostu ilości ruchu, otrzymamy
QQ^2—eQ^l= PlFl+Pl(F2~Fl)-p2F2
a po uproszczeniach
qQ(? s—®j) = (Pi-pi)F2 Podstawiając Q = F2 v2, otrzymamy = (p1~p2)F2
skąd po skróceniu przez F2 i po podzieleniu przez y otrzymamy
Pi~p2 1 s
-= -v2(y2-vl)
Obliczając różnicę ciśnień pomiędzy przekrojami 1-2 z równania Bernoułlufiu, otrzymamy
Pt—P2 1
= — iF\-v\)+hltr
Y Zg
/ porównania otrzymanych równań uzyskujemy
- «>,(©,—®!) = — («5—©J)+Artr
skąd
[6-65]
Ktr = ’T-(»a—®i) [2u2—(ł'2+®i)] = — (^2-Z’i)2
Otrzymany wzór na obliczenie strat nosi nazwę wzoru Bordy-Carnota. Uwzględniając równanie ciągłości v1F1 = v2F2 otrzymamy
III
hstr =
-2-1
2g \Fi
2g
24.1
Wyszukiwarka
Podobne podstrony:
074 075 przechodnlości relacji alesprzeczności. Proces ten przedstawiony jest na rys. 3.6. W wyniku
3.1.1. Zespół łożyska Schemat komory badawczej przedstawiono jest na Rys 9. Czop badanego łożyska (p
7 Konstrukcja przetwornika piezoelektrycznego typu "sandwich", przedstawiona jest na rys.
074 075 74 ^ ‘a przschodniości relacji niesprzeczności. Proces ten przedstawiony Jest na rys. 3>6
/ Zadanie 10 Zrealizować układ sterowania klimatyzatora. Cykl pracy układu przedstawiony jest na rys
Pętla while przedstawiona jest na rys. 27. W środku obramowania umieszcza się progr am, który wymaga
Analogowocyfrowy przetwornik I Schemat blokowy analogowo-cyfrowego przetwornika l_ przedstawiony jes
WYTYCZNE PROJEKTOWANIA ULIC- 1.4.4. Schemat węzła typu WC przedstawiony jest na rys. 9.2. Dostosowan
OMiUP t1 Gorski 9 Obraz sprężania wielostopniowego w układzie T—s przedstawiony jest na rys. 3.8. Ry
OMiUP t1 Gorski24 Budowa filtra przedstawiona jest na rys. 4.24. Wkład filtrujący 6 złożony jest z p
amat urz kr064 Układ stosowany przy omawianej modulacji przedstawiony jest na rys. 5-15. Zwykle stos
P1100243 rotacji przedstawiono jest na rys. 24.1 (jądro a) i ten typ obejmuje wszystkie o parzystej
225 (4) 225 warstw, wartość €rain(k) powinna maleć. Typowy przebieg eniin(&) przedstawiony jest
więcej podobnych podstron