22 (371)

Odchyleńia_ standardowe estymatorów bo i b\ zależą od g - nieznanej wartości odchylenia standardowego składników losowych. Oszacowaniem a jest odchylenie standardowe reszt S_c, a oszacowaniami <7_/vi i <jsą standardowe błędy szacunku parametrów

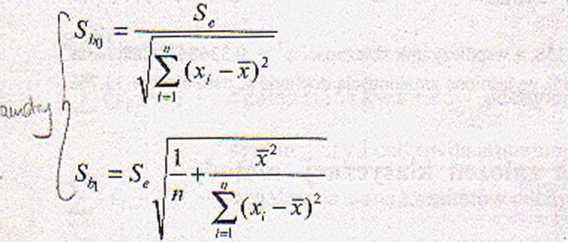
(3.23)

(3.24)

Standardowy błąd szacunku parametru informuje, o ile średnio pomylilibyśmy się in plus, lub in minus, szacując ten sam parametr modelu na podstawie różnych prób składających się z tej samej liczby obserwacji.

Standardowy błąd szacunku powinien być jak najmniejszy w stosunku do oceny parametru. W praktyce przyjmuje się, że nic powinien przekraczać 50% jego wartości, jeśli liczebność próby przekracza 20.

Przykład 3.10. W 5 firmach zbadano wartość sprzedaży i wydatki na reklamę (tab. 3.4). Tabela 3.4. Wartości zmiennych dotyczących wydatków na reklamę i wielkości sprzedaży

Nr obserwacji	Miesięczne wydatki na reklamę w USD (*)	Miesięczna wartość sprzedaży w USD (7)
l	100	i 000
2	200	1900
3	300	2700
4	400	3400
5	500	4200

Źródło: dane umowne.

Oszacowany model ma postać: 7 = 270 + 7,9* '

gdzie:

7- miesięczne wartości sprzedaży tumy w USD,

* - miesięczne wydatki na reklamę w USD.

Odchylenie standardowe reszt wynosi: S, = 60,553.

Standardowe błędy szacunku parametrów wynoszą: S =63,5 i S =0,192.

*!» ''

Gdyby parametry strukturalne oszacowano na podstawie innych prób reprezeniar-.rnyęfc 5-elemenlowych. to za każdym razem otrzymane oceny ^ i 7)j byłyhy”źape\vne różne, w rozważanym przykładzie bn średnio różniłyby się o 63,5. a b_: o 0.192.    ~

ty

vc£

>JL

S\x>.ctJUjJdL

22