243 (30)

468 Uzupełnienia

elementach grupy, symbol h oznacza deltę Kroneckera równą jedności, gdy indeksy są takie same i równą zeru, gdy indeksy są różne.

Twierdzenie Ił - o rzędzie grupy.

Niech lj oznacza wymiar nieprzywiedlnej reprezentacji i pewnej grupy symetrii, a h rząd tej grupy, czyli liczbę elementów symetrii tworzących grupę. Między wymiarami reprezentacji a rzędem grupy występuje zależność

N

£<? = />    (Ul.13)

i=\

gdzie sumujemy po wszystkich nieprzywiedlnych reprezentacjach rozpatrywanej grupy.

Twierdzenie HI - o charakterach.

Z twierdzenia o ortogonalności reprezentacji nieprzywiedlnych wynika ważne twierdzenie o charakterach: charaktery dwóch nieprzywiedlnych reprezentacji i oraz j danej grupy spełniają równanie

h

Y.XiWx>{R) = Mij    (Ul.14)

n=i

gdzie Sij oznacza symboj Kroneckera (d,_y = 1 dla i — j, 6_tj = 0 dla i ^ j), a sumujemy po wszystkich operacjach symetrii grupy. Z uwagi na to, że dla wszystkich operacji symetrii R, należących do tej samej klasy p charaktery Xi.(R_P) są jednakowe, równanie (Ul.14) zapisuje się często w postaci

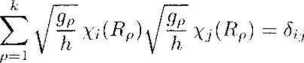
gdzie: wskaźnik p - numer klasy danej grupy, g_p - liczba operacji symetrii w klasie p, R_p - dowolna operacja należąca do tej klasy. Równaniu (U 1.15) można nadać interesującą interpretację geometryczną. Zwróćmy uwagę, że dla i ^ j ma ono postać

k

0    (Ul.16)

₍,= \

Jest to równanie wyrażające iloczyn skalarny dwóch ortogonalnych wektorów w przestrzeni wymiarowej k. Mówimy zatem, że charaktery nieprzywiedlnych

UL Elementy teorii grup punktowych

469

reprezentacji są ortogonalne, rozumiejąc przez to, że charaktery można traktować jako składowe ortogonalnych wektorów.

Z podanej interpretacji wynika bardzo ważny wniosek. Ponieważ liczba niezależnych ortogonalnych wektorów, które można utworzyć w przestrzeni wymiarowej k wynosi k, to z równania (Ul. 14) wynika, że dla danej grupy liczba nieprzywiedlnych reprezentacji jest równa liczbie klas. W rozpatrywanej grupie symetrii, do której należy cząsteczka NH3, jest sześć operacji symetrii (h — 6) i trzy klasy (k = 3). Liczba nieprzywiedlnych reprezentacji dla tej grupy wynosi więc trzy, a na podstawie równania (U 1.14) suma kwadratów wymiarów tych reprezentacji wynosi sześć. Jest tylko jeden możliwy sposób przedstawienia liczby sześć jako sumy kwadratów trzech liczb całkowitych, tj.: 6 = l² + l²4-2². W rozpatrywanej grupie występują więc dwie reprezentacje jednowymiarowe i jedna dwuwymiarowa. Więcej nieprzywiedlnych reprezentacji nie ma.

Ortogonalność charakterów można wykorzystać do wyprowadzenia prostego i ważnego wzoru dotyczącego reprezentacji przywiedlnych. Naszym celem jest znalezienie krotności występowania reprezentacji nieprzywiedlnej w reprezentacji przywiedlnej.

Twierdzenie IV - o liczbie reprezentacji nieprzywiedlnych w reprezentacji przywiedlnej.

Mówiliśmy, że każdą reprezentację przywiedlną można rozłożyć na reprezentacje nieprzywiedlne

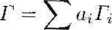
(Ul. 17)

Oznacza to, że charaktery tej przywiedlnej reprezentacji ;y(/?) wyrażają się jako sumy charakterów odpowiednich reprezentacji nieprzywiedlnych

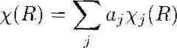
(Ul.18)

Jeśli pomnożymy obie strony tego równania przez Xł(6^>), wysumujemy po II i skorzystamy z równania (U 1.14), to otrzymamy

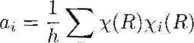
n

(Ul.19)

Korzystając z tego wzoru można dowolną reprezentację przywiedlną rozłożyć na nieprzywiedlne, czyli odpowiedzieć na pytanie, ile razy reprezentacja nie-