26

52 ..Ćwiczenia laboratory jne z mechaniki płynów’’

ziemskiego. „Powierzchnie ekw ipotencjalne" są jednakowymi paraboloida-mi obrotowymi. Powierzchnią ekwipotencjalną jest również swobodna powierzchnia cieczy, która może być łatwo poddana obserwacji. Wszystkie punkty na swobodnej powierzchni cieczy , w tym również punkt A poddany jest działaniu dwu sił: przyspieszenia ziemskiego i odśrodkowego.

W równaniu równowagi pły nu

(1)

d p = p (Xdx + Ydy + Zdz)

gdzie: p - gęstość cieczy. p - ciśnienie cieczy,

X, Y, 7. - jednostkowe siły masowe w kierunku osi jr,y, z składowe jednostkowej siły masowej dla przypadku naczynia wirującego wokół osi pionowej mają następującą postać:

(2)

X -r0²,

K = 0.

Z = -g.

Uwzględniając zależności (2) w (I) mamy :

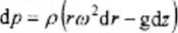
V    ż

O)

po scałkowaniu:

(4)

Stałą całkowania C można wyznaczyć z warunku, że dla r - 0 i ~ - z_a (punkt na powierzchni cieczy' na osi naczynia) jest:

P= Pa= Pa-

Wtedy:

^C = Pa+PgZ₀

Po podstawieniu zależności (5) do (4) otrzymuje się ostateczne równanie:

Porwała ono obliczyć ciśnienie cieczy wirującej w stanie równowagi względnej w dowolnym punkcie o w spółrzędnych r, z wtedy, gdy znana jest rzędna z_a powierzchni swobodnej cieczy dla r -0, ponad którą panuje ciśnienie

atmosferyczne p_a.

Rozkład ciśnienia wzdłuż dowolnej prostej pionowej można obliczyć dla stałej prędkości kątowej <y = const, przyjmując w równaniu (6) r - const. Rozkład ciśnienia wzdłuż takiej prostej jest liniowy i zależy tylko od współrzędnej z, tzn. p = p(z). Podobnie dla dowolnej prostej poziomej r - const.

otrzymuje się z równania (6) paraboliczny rozkład ciśnienia p - p{r~).

W celu wyznaczenia równania powierzchni ekw {potencjalnych (izoba-rycznych) należy w równaniu równowagi cieczy wirującej wokół osi pionowej^). przyjąć dp - 0.

Mamy wówczas:

rw'dr~ gdz — 0

po scałkowaniu:

Stała całkowania C wynika z warunku, że dla r - 0 jest z = z_a. stąd

C =•—gr_n.

Stąd po podstaw ieniu otrzymuje się równanie:

(7)

P - Pa ⁺ P

rV

+ %(z_a-z)

(6)

rV

2 g

Jest to równanie paraboloidy obrotowej o wierzchołku przesuniętym o rzędną z_a względem początku układu współrzędnych. Wszystkie takie powierzchnie ekwipotenejalnc tworzą zbiór identycznych powierzchni przesuniętych względem siebie wzdłuż osi Z. Kształt powierzchni ekwipotencjalnych nie zależy od gęstości (a więc od rodzaju cieczy ).