290 (12)

W układzie równań (15.10) szukanymi wielkościami są szerokość i długość pozycji obserwowanej (<p_ę i X_t).

Rozwiązanie tego typu układu równań z dwoma niewiadomymi nie jest zbyt proste, ponieważ może powstać dwuznaczność. Koła pozycyjne bowiem przecinają się w dwóch punktach. Aby uniknąć dwuznaczności, wprowadza się pomocnicze kąty

<

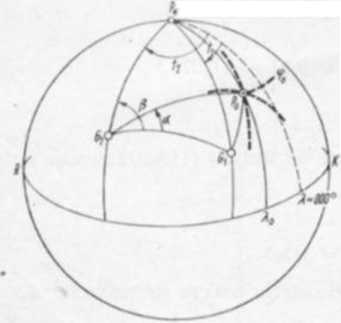
Rys. 15.14. Analityczne określanie współrzędnych pozycji obserwowanej z przecięcia się dwóch kół pozycyjnych na sferze niebieskiej

a i fi w trzech trójkątach sferycznych, które powstają przez połączenie gwiazd G_{ \ G₂ 7 P₀ (rys. 15.14). Na tej zasadzie oparte są metody Djakonowa [2] i Kotlari-ća [wg 3).

Do innej grupy metod analitycznego określania współrzędnych pozycji obserwowanej należą metody Dcnisowa [wg 3] i Flynna [4].

Metoda Flynna jest warta uwagi, ponieważ za jej pomocą można łatwo obliczyć pozycję, używając elektronicznych maszyn cyfrowych.    *

Podstawowe zależności tej metody są następujące:

sin 6 * cos h, • cos <p₀ • cos A + sin (p₀ • sin/i,,    (15.11)

• /. . , v — cos h.* sin .4    ... ...

sin(f₀ + *_#) --^-.    (15.12)

srnd

Z zależności (15.11) oblicza się cos²/!, a z zależności (15.12) oblicza się sin²/!. Przekształcone w ten sposób równania dodaje się stronami, uzyskując zależność

cos²£ • sin²(f₀-f X₀) • cos² ę>_#+(sin$-sin<p₀ • sin h,)² —

—cos²p_# • cos²h_a = 0.    (15.13)

Wyrażenie (15.13) jest parametrycznym równaniem stożka, którego wierzchołek znajduje się w środku Ziemi. Przecięcie się bocznej powierzchni tego stożka z powierzchnią Ziemi daje koło jednakowych wysokości o promieniu 90°—h_a.

Dla obserwowanych dwóch ciał niebieskich otrzymuje się dwa równania, w których niewiadomymi są współrzędne pozycji obserwowanej P₀ {<p_ot 2,). Współrzędne pozycji obserwowanej P₀ (<p_0t z reguły różnią się niewiele od współrzędnych pozycji zliczonej P_m (f,, ż,), stąd różnice A(p i AX są również nieduże.

290