360 (5)

gdzie

A ii	0	>11	0	A ii Ai(,i)
.A KII)	1_	0		. ^0ln

^AIl^I>!l^All    Aj[5 P_([ A _[(|ł)

r    t

Aj (ii) ^*ii A|i A_i(11) Pj] A_I([I) +P^_i

APL =

A ii	0	>11	0	Lj[
aT ^akh)	V.	0	^p*,_

A ii P|[ L||

Af(U) Pu L|j -P^d*,

Zatem

^a^i(n>

AlP„A„

A || Pji A

K»)

^A l(ll) ^p[| A j] A_I(11) P_n A_I(I()+P^

A II Pm L

I! ^r II A| (ji) Pu L_n

(7.16)

o macierzy kowariancji (na podstawie wyrażenia d _Y =-(A⁷ PA)”¹ A⁷ PL = DL oraz modelu C_L = C^_llh =<Tq P“‘)

^ca._v =DC_LD⁷’«DC_tl*D^r = (A ^rP A) ~^{A ⁷ PC PA (A ⁷ P A) ~¹ =

~ C7q (A⁷'pA)”‘ A^rPP"^IPA(A⁷’PA)-‘ =

= or?(A^rPAr'

Biorąc pod uwagę, że

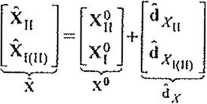
X = X° =d_r

oraz zastępując współczynnik wariancji <Tq jego estymatorem

O

»’ó =

V^rPV

/

uzyskujemy

^Cx=C- =/«6(A'PA)-' - md

Ali Pn Ai

A P„ A,

i! Ml'Ml *'MI ¹ II -'M (II) ^Al(ll)^ł>!l ^Al! ^AI(I!)^I>II ^AI (II) ^ł’^I>x,

(7.17)

W celu ustalenia liczby stophi swobody f formy kwadratowej V¹ PV powróćmy do rozdz. 3.2.2. Wykazaliśmy tam, że

/ = Tr(M) =--n~r

gdzie M - I„ ~ A(A¹ PA)^-1 A⁷ P. W naszym problemie

(A 9l^,l,r) => A.¹ PA 6 ^,r «=«„+#■,.    r = r_n+r_{

gdzie (przypomnijmy):

/i i [ — liczba nowych pomiarów,

z-, - liczba parametrów pierwotnej sieci geodezyjnej (elementów wek-

^tora ‘W-,

/•[[ - liczba nowych parametrów (elementów wektora Zatem

/ = Tr(M) - Tr(I_/J|1+a)-Tr[A⁷ PA(A⁷ PA)”⁵1 =

“ ^ ^(1 ;|[j fl-j ) ~ 1    i-^ ) ~

“ ("n '⁽'^ri)"(^rn ^+ri)⁼ "u ~'ii

Wobec tego

-> V^rPV

'"()•=-- (7.18)

«n -hi

(zobacz także Gkebiennik 1981). Warto zauważyć, że w modelu macierzy kowariancji C_LC_xu/,, wielkość o"d jest wspólnym współczynnikiem w obu lokalnych modelach

Ctf^O²^. C_S( = <7() (Aj PjAj)"¹

stanowiących przekątniowe bloki macierzy kowaiianeji C_x„/>. Można zatem spodziewać się nieco innych wartości tego współczynnika w porównaniu z wynikami uzyskiwanymi w wyrównaniu łącznym. Natomiast prawidłowym, z teoretycznego punktu widzenia, postępowaniem jest przyjęcie dwu lokalnych współczynników wariancji oraz wyznaczenie ich wartości z zastosowaniem