33 (500)

r o

Optyka

Interferencja i dffral«£ja iwiaftta

Przeczytaj uważnie poniższy tekst i wykorzystaj do rozwiązania zadań.

Rozwiązując zadania do paragrafu „Zasada Huygensa. Interferencja i dyfrakcja fal” przypomniałeś sobie warunek maksymalnego wzmocnienia inter-ferujących fal spójnych. Ma on postać

\r₂--fil*/U, n = 0,1,2,...

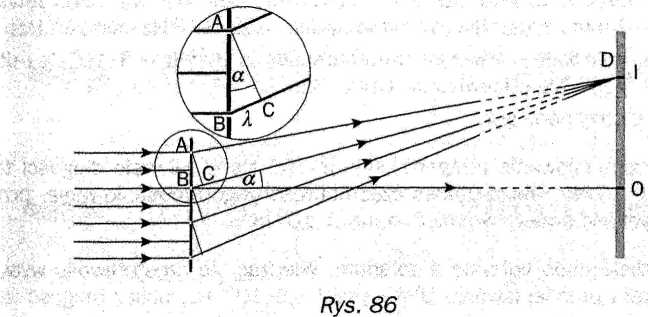
W tym wzorze r_x i r₂ to odległości punktu, w którym spotykają się fale, od ich źródeł. Na rysunku 86 pokazano układ szczelin, przez które przechodzą fale świetlne, które następnie nakładają się. (Uwaga: na rysunku nie zacho-

Optyka

wano proporcji. Siatka dyfrakcyjna ma bardzo małe rozmiary w porównaniu Z Jej odległością od ekranu.)

Zauważ, że różnica odległości od źródeł r₂ - r₁ jest równa AB - sina. Tak więc warunek wzmocnienia możemy zapisać jako

a sin a = nA ,

gdzie:

AB -a - odległość między sąsiednimi szczelinami,

A - długość fali,

n - numer prążka otrzymanego po przejściu światła przez szczelinę,

« - kąt między kierunkiem pierwotnej wiązki i promieniem, który w wyniku interferencji daje prążek n - tego rzędu.

Na ekranie można zobaczyć tylko takie prążki, dla których a < 90°, a więc

a • 1

sina< 1. Maksymalny rząd widma n_max < —— oraz n_max jest liczbą całkowitą.

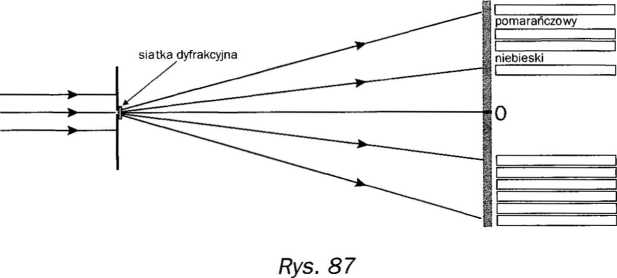
31 ^<i. Na siatkę dyfrakcyjną pada wiązka światła białego (rys. 87). W odległości / od siatki na ekranie pojawia się widmo I rzędu. Wpisz w puste miejsca odpowiednie barwy otrzymane na ekranie. (Uwaga: na rysunku nie zachowano proporcji. Siatka dyfrakcyjna jest bardzo mała w porównaniu z jej odległością od ekranu.)

11©. Oblicz długość fali światła laserowego, które po przejściu przez siatkę dyfrakcyjną daje na ekranie tylko prążki I i II rzędu. Stała siatki a= 0,0025mm, sina,, = 0,6.

B21₀ W doświadczeniu Younga użyto światła monochromatycznego o długości fali A = 600nm. Oblicz liczbę otrzymanych na ekranie prążków, po przejściu światła przez szczeliny. Odległość między szczelinami wynosi a = 2jum.