340 (26)

562

Grammel¹ udowodnił w 1947 r., że do oceny wytrzymałości tarczy na eksplozję odpowiednim wskaźnikiem jest średnie naprężenie obwodowe tarczy. W zadaniu nie musimy się zajmować składowymi promieniowymi a,.

Napiszmy równanie równowagi wycinka tarczy między promieniami r_w, r_t, ograniczonego kątem dtp (rys. XIV. 18):

___ dtp

2Tsm~ = Tdtp = r_t-r_w+dC.    (XIV.84)

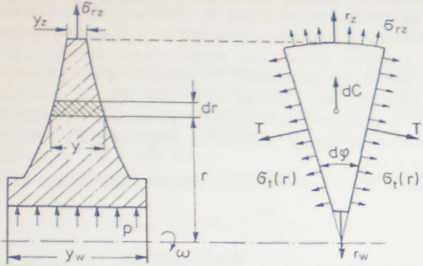
Rys. XIV. 18. Naprężenia i siły działające na wycinek tarczy

Podstawiając odpowiednie wyrażenia i upraszczając przed dtp otrzymamy

^r«    r |

J <r,-y-dr = (y_x r_s-<T_rz+y_w‘r_w-p)+Q(o² J r¹ydr.    (XIV.85)

^rw    r_w

W przypadku tarczy bez otworu albo bez wcisku drugi wyraz po prawej stronie zeruje się, y_wr_wp = 0. Ze wzrostem prędkości obrotowej powyżej wartości nominalnej co > to₀ zmienia się wyraz pierwszy i trzeci po prawej stronie:

o(ś0.    0)

QCO^Z = QCJ}1    (2)

Równanie (XIV.85) można napisać w postaci (przy y_wr_wp = 0):

Ś a_t-y dr = y_x r_x o_n0(—+0£Oo(~^>) • J r²ydr. (XIV.86)

\®0/    \^W0/ r„

Ze wzrostem co > co₀ rośnie naprężenie a, i może osiągnąć granicę plastyczności na promieniu wewnętrznym przy pewnej wartości co * co. Dalszy wzrost prędkości co > co' powoduje odkształcenie plastyczne na promieniu r„, które rozszerza się w kierunku rosnących promieni, aż osiągnie całość tarczy (rys. XIV.19). W tym stanie, przy prędkości u) = co, w obrębie całej tarczy, naprężenie obwodowe będzie równe granicy plastyczności. Ponieważ przy założonej idealizacji granica wytrzymałości doraźnej jest równa granicy plastyczności

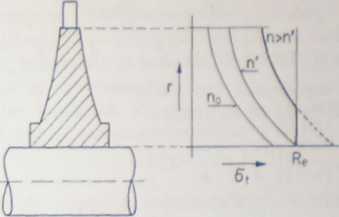
Rys. XIV. 19. Rozkład naprężeń w tarczy a, po osiągnięciu granicy plastyczności na promieniu

wewnętrznym

dochodzimy do sytuacji prowadzącej do pęknięcia całej tarczy jednocześnie, czyli do eksplozji tarczy.

W rozpatrywanych warunkach wirnik pęka natychmiast, a nie po upływie pewnego czasu.

Podstawiając w równaniu (XIV.86) co = co, oraz a, = R,. znajdujemy wzór

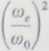
R/jydr

r_a

y_t-r_t-<j_no+e<Oo ! r²ydr

(XI V.87)

pozwalający obliczyć prędkość eksplozji co,.

Tak obliczona prędkość co, powinna być przynajmniej o 25-r30% większa od prędkości odwirowania wirnika, tj. przynajmniej 50% powyżej największej wartości co_max występującej podczas eksploatacji. Zauważmy, że równanie (XIV.87) na coj(o₀ nie zawiera wyrazów zależnych od temperatury. Prędkość eksplozji co, nie zależy więc od rozkładu temperatur w tarczy i od naprężeń termicznych. Mają one jedynie wpływ na rozkład wydłużeń plastycznych w chwili osiągnięcia przez tarczę pełnego stanu plastycznego.

1

Grammel R., Die Erklarung des Problems der hohen Sprengfestigkeit umlaufender Scheibe, Ing. Archiv, 1947, 1.