404 (4)

(Ady + L)⁷ M(Ad,y +L) = min

*    -y    ~ y

li tl X ii N ~ d .r N d X ~ ^m>n

W nawiązaniu do zasad rachunku wyrównawczego, sprzeczny układ równań Ad_v +L = 0 zastępujemy, jak wiadomo, układem równań poprawek Ady + La V, akceptując w ten sposób reszty jego rozwiązania (w takim ujęciu, wektor poprawek jest wektorem reszt lub, inaczej, wektorem residuum, zob. przykład 1.24). Przyjmijmy również, że M = P jest macierzą wag wektora wyników pomiaru (a tym samym wyrazów wolnych L), natomiast N = P_x, ustalmy na razie ogólnie, macierzą wag znanych przed wyrównaniem współrzędnych punktów. Wówczas

d _v = - A L - -A L

jest takim rozwiązaniem układu równań poprawek, że

V⁷ PV = min d_xP_xd_x = min

Powróćmy teraz do omawianego przykładu. Otóż jeśli przyjmiemy, że w swobodnym trójkącie wektor d _v ~[dx_x tiy_Zx ^ x_?1 ^cIy_/? ^x_z    ⁽W-_/x

jest nieznanym wektorem przyrostów do przybiiżonych współrzędnych wszystkich punktów oraz że P_x jest diagonalną macierzą wag tych współ-

«'p    *

rzędnych, to własność d_xP_xd_x=min można przedstawić w następującej szczegółowej postaci:

d⁷_vp_xdy =l>Xy^²x_A ⁺PYz_[ \ ⁺PXz₂^X_Z2 ⁺

^{+ Py}*A₂ ^+Pxz/^lXy., ^¥pw\ ^=min

Wyrównanie swobodnej sieci geodezyjnej, z zastosowaniem rozwiązania d_x =-App ,L, polega więc z jednej strony na wyznaczeniu takich przyrostów d^, że ę(d,y ) = V⁷ PV = min (tak jak dotąd), natomiast z drugiej

na optymalnym (w sensie kryterium d_xP_xd_x = min) wpasowaniu sieci wyrównanej w sieć przybliżoną, przy czym rola poszczególnych punktów sieci przybliżonej w procesie optymalizacji może być sterowana (regulowana) macierzą wag P_x (rys. 9.1c).

b) wyrównanie klasyczne

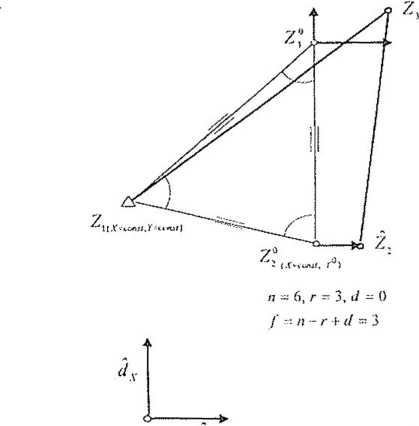
/i -• 6, r 6, il ~ 3 / n - r t- 4    3

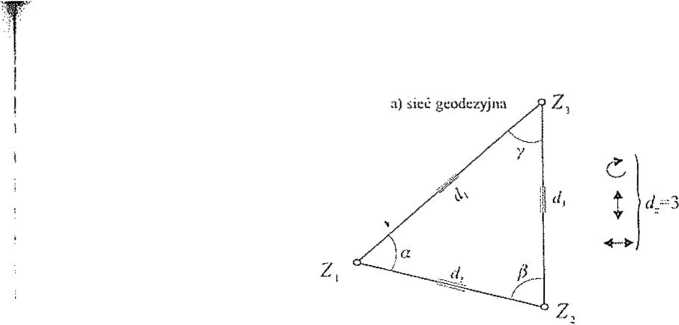
c) wyrównanie swobodne

£    ■ ■■ przemieszczenie wzdłuż osi X

■4—> ■■■• przemieszczenie wzdłuż osi Y - obrót

dy    Z,, Z.. Ź, - punkty o wyrównanych współrzędnych

Rys. 9.1. Ilustracja założeń wyrównania swobodnego

Wyrównanie swobodne, oprócz optymalnego wpasowania sieci wyrówna-nej w sieć przybliżoną, pozwala także na uniknięcie subiektywnej oceny dokładności położenia punktów w sieciach swobodnych. Jak już wcześniej wskazywaliśmy na przykładzie sieci geodezyjnej w układzie (X, Y), w klasycznym wyrównaniu defekt zewnętrzny jest eliminowany przez przyjęcie jako stałych odpowiednich współrzędnych wybranych punktów (lub współrzędnych jednego punktu i azymutu dowolnego boku sieci). W swobodnych sieciach niwelacyjnych t/, - 1, z czego wynika, że układ współrzędnej B jest jednoznacznie definiowany przez przyjęcie wysokości tylko jednego z punk-

405