45

90 .Ćwiczenia laboratoryjne i mechaniki płynów”

l - czas.

Przepływ lam mamy w znacznej (niległości od wlotu rury charaktery zujący się współosiowymi równoległymi powierzchniami prądu istnieje, jeżeli liczba Rey noldsa wyznaczona dla tego przepły wu, określona zależnością (5), spełnia warunek

(8)

Re <2300.

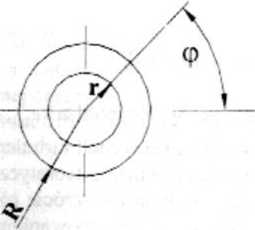
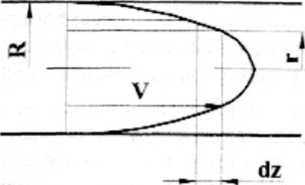
Rys. 3. Przepływ laminamy w kanale o przekroju kołowym.

Warunek powyższy otrzymano na drodze badań empirycznych. Ten rodzaj przepływu nazywany jest przepływem Hagena-Poiseuille'a. Przepływ w kanale o przekroju kołowym wygodnie jest rozpatrywać w biegunowym układzie współrzędnych r,<p,z. Zakłada się. że przepływ jest osiowo-symetryczny i dlatego pomija się zmiany parametrów^ przy zmianie kąta <p (ry s. 3).

Pełną postać równania ciągłości i równań N-S zapisanych w różnych układach współrzędnycłi można znaleźć w literaturze. W dalszej części instrukcji zostaną one przedstawione po uwzględnieniu założeń upraszczających w układzie /•,«», r.

Dla przepływu lam marnego przy jmuje się, że składow e w ektora prędkości w kierunkach obwodowym i promieniowym równe są zeru, czy li

%=0 i v_r = 0.    (9)

W wyniku powyższych założeń z równania ciągłości otrzymuje się zależność

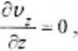
a więc prędkość v. istniejąca na danym promieniu r nie zmienia się wzdłuż osi "

Zakładając, żc /miana gęstości płynu wynikająca z różnicy ciśnień na wlocie i wylocie kanału jest pomijalnie mała. równania N-S w układzie biegunowym. po uwzględnieniu zależności (9) i (10). redukują się do postaci

dv

OD

^J^(rir-^)=^C£-r, cr ar cz

^=o.

dr

Drugie z równań układu (11) mówi o niezmienności ciśnienia wzdłuż promienia rury dla danego r. Pierwsze równanie obrazuje równowagę sił ciśnienia wywołujących przepły w i sił tarcia. które go hamują.

Rozpatrując tę równowagę dla nieskończenie cienkiego walca (rys.3) o powierzchni 2-rdr i uwzględniając hipotezę Newtona (zależność Newtona (1)). otrzy muje się

2xrdzrj--j— dr .    (12)

dr    dr

Po zróżniczkowaniu zależności (12) względem r otrzymuje się pierwsze równanie układu równań (11). Ponieważ v_ nie zależy od z. to różniczkując

to równanie względem z otrzymuje się

^4 = 0.    (13)

dr‘

Rozwiązaniem równania (13) jest funkcja liniowa względem z, czy li zmiana ciśnienia wzdłuż długości kanału jest liniowa. Inaczej mówiąc, strata ciśnienia na jednostkę długości kanału jest stała, przy czym dodatnim przyrostom r towarzyszy spadek ciśnienia. Powyższe można opisać następującym związkiem

d p *P_W dr /    ’

gdzie / oznacza odcinek długości kanału, na który m następuje strata ciśnie-nia Ap .

• tir