4 (1052)

Tarcie cięgien

Dane jest giętkie, nierozciągliwe cięgno, stykające się z powierzchnią walca kołowego wzdłuż luku ADB odpowiadającemu kątowi środkowemu a , zwanemu kątem

opasania, jak na rysunku.

A

dN

dT    dł== R'dq>

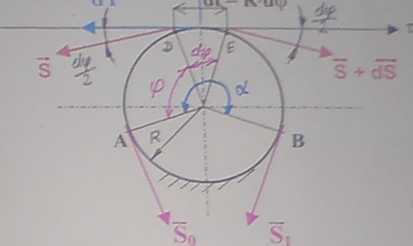
Współczynnik tarcia cięgna o walec jest równy u. Do jednego końca cięgna przyłożona jest siła S|. Należy znaleźć najmniejszą siłę S>, którą trzeba przyłożyć do drugiego końca aby zachować równowagę sil.

Rozpatrzmy w tym celu równowagę sił przyłożonych do nieskończenie małego elementa DE o długości dl = R- dtp gdzie R jest promieniem walca. Na r Ir went In działają stły naciągu S + dS i S w punktach D i E, normalna reakcja d S i siła tarcia dT.

Z warunku równowagi elementu mamy:

XP_it = (S + dS) - cos ^ - S-cos ^ - dT =0 ZP_to = dN I (S + dS) • sin ^ - S sin ^ = 0

(i)

(2)

Przyjmując, że: sin — = —

COS — = 1 2

(3)

po uporządkowaniu mamy:

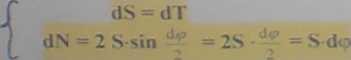
Rozważamy przypadek równowagi granicznej dlatego na kontakcie walca i cięgna występuje tarcie rozwinięte. Obowiązuje zatem związek:

a dalej, po wstawieniu do (3) dłś — dT ³ 5.1-dN ^ Srdtg