68 (17)

128

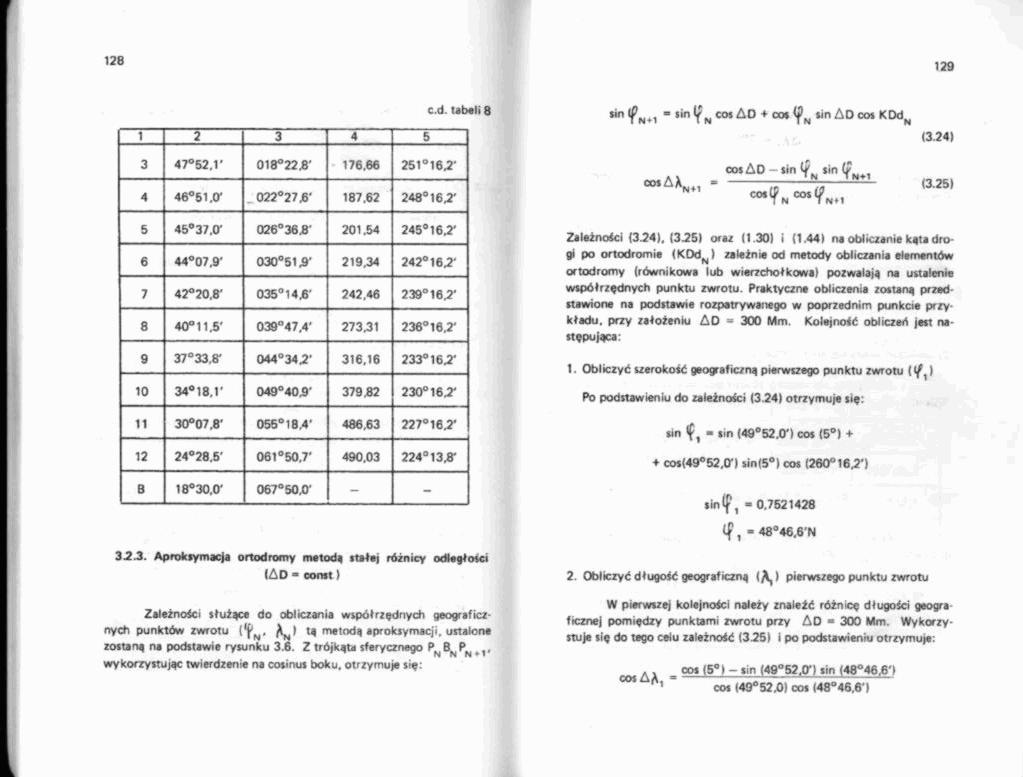
c.d. tabeli 8

1	2	3	4	5
3	4 7° 52.1*	018° 225'	* 176.66	251° 165'
4	46° 51.0*	022°275'	187.62	248° 165*
5	45°37.0*	026°365'	201.54	245°16.2*
6	44° 07,9*	030°515'	219.34	242° 165'
7	42° 20.8'	035° 14.6'	242.46	?39°165*
8	40° 11.5*	039°47.4'	27351	236° 165*
9	37°33.8'	044°345*	316.16	233° 165'
10	34°18.1*	049° 405’	37952	230° 165*
11	30°07.8'	056° 18.4*	486,63	227°165*
12	24°28.6*	06ł°50.7'	490.03	224° 135*
B	18° 30,0'	067° 50.0'	-	-

32.3. Aproksymacja ortodromy metodą stałej różnicy odległości

(AD • comt)

Z*le*nośc> służące do obliczenie współ rządnych geografie* nych punktów zwrotu lf_N. tą metodą eproksymecji. ustalone zosteną ne podstawie rysunku 3.5. Z trójkąta sferycznego P_N6_NP_N#1, wykorzystując twierdzenie ne cosmus boku. otrzymuje sią:

pn tp_Nł1 • sin (f _n cos AO ♦ cos    cos ^KDd*

(3.24)

(3.25)

cos AD — >1n <f_N

^N" ‘

Zależności (3 24). (3-25) oraz (1 30) i (1 44) ne obliczanie k«ta dro gł po ortodromie (KDd..) zależnie od metody obliczenie elementów

W

ortodromy (równikowa lub wierzchołkowe) pozwalaj* ne ustalenie współrzędnych punktu zwrotu. Praktyczne obliczenie z o* tan* przed stawiona na podstawie rozpatrywanego w poprzednim punkcie przykładu. przy założeniu AO - 300 Mm. Kolejność obłiczaó |est następująca:

1. Obliczyć szerokość geograficzne pierwszego punktu zwrotu («/,)

Po podstawieniu do zależności (3.24) otrzymuje ste-

słn $ _f - sm (48®52.0*) cos (5°) ♦

♦ cos(49®52.0*) sin(5°) cos (260° 162*)

sin(f, - 0.7521428 tf _f - 48°46.6'N

2. Obliczyć długość geograficzna (A,) pierwszego punktu zwrotu

W pierwszej kolejności należy znaleźć różnce długości geogra licznej pomiędzy punktami zwrotu przy AO - 300 Mm. Wykorzystuje sie do tego celu zależność (325) I po podstawieniu otrzymuje:

cos AA,

oot (S°) — sin (49°S2.fr) sin (48°46^) cos (40*52j0) cos (48°46.6 )