70 71 (31)

70 Cifit I. Wpranlmlt d<> ekonomii

2.7.3.1. Mierzenie cenowej elastyczności popytu

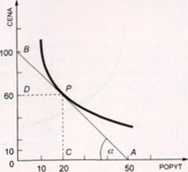
R«\unek 2JI. Mierzenie cenowej ctatyc/noici pop>tu

Chcemy zmierzyć cenową elastyczność typowej funkcji popytu, której graficznym wyrazem jest krzywa przedstawiona na rysunku 2.21. Wychodzimy ze wzoru (2.3) na cenową elastyczność popytu, który zapisujemy:

(2.14)

F    Ac    AP, c

⁼ P_F ■ c    Ac ' P_F

Nachylenie typowej krzywej popytu w punkcie P przybiera (zgodnie z kon-, . .    .    OB 100    _i

wencją matematyczną) wartości ujemne i wynosi    = - 2. Do ob*

Ac

Ac

liczenia elastyczności potrzebna nam jest odwrotność ——, gdyż

, AŁ

Ac '

popytu mierzona w- punkcie P wynosi więc:

n 60    60 ₌_3

^“ \ 2 / 20    40    2'

Analogiczny wynik (w wartościach bezwzględnych) otrzymamy, stosując przybliżone trzy metody jej mierzenia (bierzemy odwrotność stosunków z poprzedniej strony):

AC 30    3    OD 60    3^    .    .^Ap 42    3

0C 20 ^- 2’    ’ 40 “ 2¹    ’ J>B “ 28 ~ 2'

Elastyczność cenową popytu możemy obliczyć bez uciekania się do graficznej prezentacji, korzystając z pojęcia pochodnej.

Przyjmijmy, że funkcja popytu ma postać: P, = /(c). gdzie: c - cena. Niech przykładowo P_t = 2Q-2c. Obliczamy pochodną tej funkcji f'(c). Wynosi ona: f\c) » - 2 dla każdego c >0.

Przyjmijmy, że cena wynosi 4. Wtedy, korzystając z formuły (2.13). którą zapisujemy teraz:

(2.15)

^rp

stąd otrzymujemy:

F = 2    ⁴    ₂    ⁴    2 —    —    -■

20- 2 4    20- 8 ⁼”    12" 12* 3'

zaś przy cenie c = 5:

F 2    ⁵    2    ⁵—    ,

20-2-5    20-10*' 10'

Ujemny współczynnik cenowej elastyczności popytu informuje, że cena i popyt zmieniają się w przeciwnych kierunkach. Jest to. jak pamiętamy z wcześniejszych rozważań, typowe zachowanie się popytu.

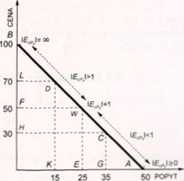
R)-»ai»rk 2.22. Elastyczność wzdłuż liniowej funkcji popytu

Przyjmijmy teraz, że krzywa popytu ma kształt linii prostej, czyli jest graficznym odzwierciedleniem liniowej funkcji popytu (rys. 2.22). Pozwoli to w sposób wyraźny przedstawić różnicę między nachyleniem a elastycznością.

Jak pamiętamy, nachylenie prostej jest stale w każdym punkcie. W naszym przykładzie wynosi:

1