70

140 „ćwiężenia laboratoryjne i mechaniki płynów''

1 - jednostkowa długość walca o przekroju kołowym.

Wówczas:

(2)

P_c = \p cos(n,v_x)dl l

P₍ - siła przypadająca na jednostkę długości opisywanego walca.

Sił) styczne (oprócz tarcia powierzchniowego) zwrócone są zgodnie 7 prędkością względną płynu. Składowa tych sił w kierunku prędkości niezakłóconej Uq nazywa się oporem tarcia P₍.

Wyrażamy go w sposób następujący:

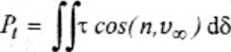
5

Po przejściu podobnych uproszczeń jak wyżej wzór (3) można zapisać następująco:

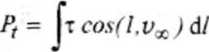
(4)

gdzie:

(l,v^) - kąt między styczną do obwodu profilu (mającą ten sam zwrot co t a kierunkiem prędkości t- naprężenia styczne spowodowane lepkością cieczy'.

Wprowadzając pojęcie ciśnienia dy namicznego

v

Pj = P -

i oznaczając powierzchnię odniesienia przez S można uprowadzić bezwymiarowe współczynniki oporu ciśnieniowego i oporu tarcia:

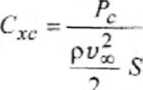
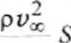
7

(6)

Wielkości tych współczynników zależą od kształtu ciała, liczby Reynoldsa i liczby Macha.

Warunkiem wyznaczenia oporu ciśnienia bądź oporu tarcia jest uprzednie wyznaczenie rozkładu ciśnienia na powierzchni wzdłuż profilu p = p(l) i rozkładu naprężeń stycznych x = 1 (l /. Najprostsza metoda teoretyczna obliczeń ciśnienia polega na założeniu, żc przepływ jest potencjalny. Dla profilu kołowego rozkład ciśnień na po-wierzchni określić można wg wzoru:

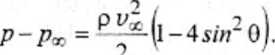
(7)

gdzie:

p<x> - ciśnienie statyczne strumienia niezakłóconego B - kąt określający położenie punkt na profilu (rys. 3)

p - gęstość powierza opły wającego profil; p = ——.

RT

Metoda obliczenia współczynnika oporu ciśnieniowego, lub oporu tarcia wymaga znajomości rozkładu ciśnienia wzdłuż profilu. Dla przepływu potencjalnego taki rozkład można obliczyć teoretycznie, przepływ rzeczywisty jest jednak daleki od potencjalnego. Dlatego aby otrzymać funkcję pfl)lubx(l)dokonuje się pomiaru rozkładu ciśnień w^ określonym punkcie profilu (rys. 4).