7

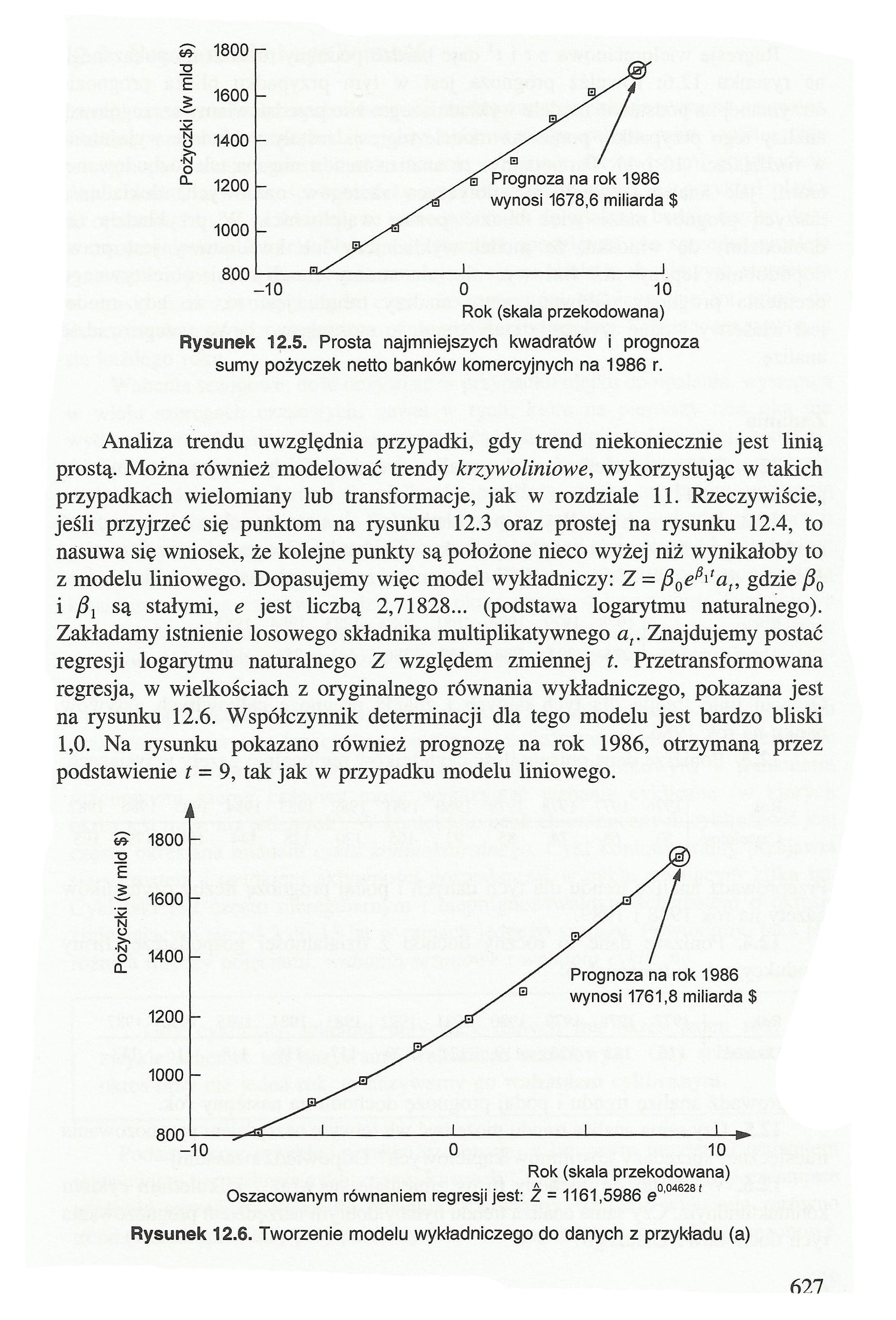
Rysunek 12.5. Prosta najmniejszych kwadratów i prognoza sumy pożyczek netto banków komercyjnych na 1986 r.

Analiza trendu uwzględnia przypadki, gdy trend niekoniecznie jest linią prostą. Można również modelować trendy krzywoliniowe, wykorzystując w takich przypadkach wielomiany lub transformacje, jak w rozdziale 11. Rzeczywiście, jeśli przyjrzeć się punktom na rysunku 12.3 oraz prostej na rysunku 12.4, to nasuwa się wniosek, że kolejne punkty są położone nieco wyżej niż wynikałoby to z modelu liniowego. Dopasujemy więc model wykładniczy: Z =    gdzie /3₀

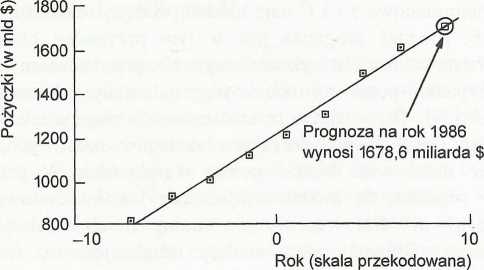
i /?j są stałymi, e jest liczbą 2,71828... (podstawa logarytmu naturalnego). Zakładamy istnienie losowego składnika multiplikatywnego a_r Znajdujemy postać regresji logarytmu naturalnego Z względem zmiennej t. Przetransformowana regresja, w wielkościach z oryginalnego równania wykładniczego, pokazana jest na rysunku 12.6. Współczynnik determinacji dla tego modelu jest bardzo bliski 1,0. Na rysunku pokazano również prognozę na rok 1986, otrzymaną przez podstawienie t = 9, tak jak w przypadku modelu liniowego.

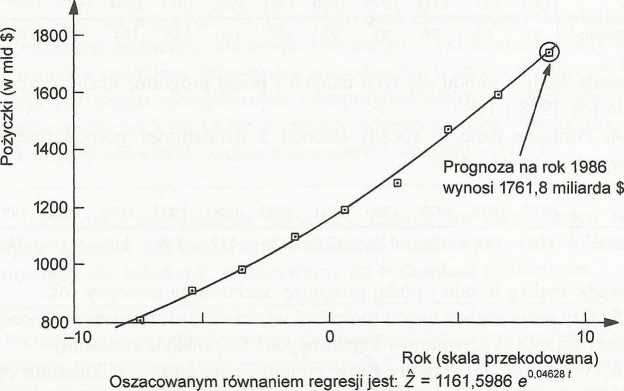
Rysunek 12.6. Tworzenie modelu wykładniczego do danych z przykładu (a)

627