9

analizy w naszym przypadku jest uzależnione od ustalenia (obliczenia) brakujących prawdopodobieństw, w tym: prawdopodobieństwa znalezienia ropy w przypadku pozytywnego wyniku testu, prawdopodobieństwa nieznalezie-nia ropy w przypadku pozytywnego wyniku testu, prawdopodobieństwa znalezienia ropy w przypadku negatywnego wyniku testu oraz prawdopodobieństwa nieznalezienia ropy w przypadku negatywnego wyniku testu. Rozpoczniemy od obliczenia prawdopodobieństwa znalezienia ropy w przypadku pozytywnego wyniku testu, przyjmując, że:

X oznacza znalezienie ropy,

X_n oznacza nieznalezienie ropy,

Y oznacza pozytywny wynik testu,

Y_n oznacza negatywny wynik testu.

Z 2. prawa rachunku prawdopodobieństwa mamy:

p (XiY)=p (X)*p(Y/X) i p(YiX)=p (Y)>p(X/Y)

a ponieważ prawdopodobieństwo wystąpieniami Ymusi być takie samo jak prawdopodobieństwo wystąpienia Y i X, to

p(X)*p(Y/X) = p(Y,)* p(X/Y)

zatem

p(x/n pW'p(^y/V

^{P (X Y)}~    P OO

Z kolei z 3. prawa rachunku prawdopodobieństwa mamy: P{Y)-P (Y/X) 'p(X) + p (Y/X_n) «p(X„) pamiętając, ±tX_n oznacza nieznalezienie ropy, przy czym

p (X_n) = 1 -p (X)

Ostatecznie zatem mamy:

p{X/Y) =

p(X)>p(Y/X)

p (Y/X) *p{X)+p(    «p ,,)

Równanie to jest regułą Bayesa. W naszym przykładzie jego poszczególne symbole oznaczają:

p (X/Y) - prawdopodobieństwo znalezienia ropy, jeżeli wynik testu sejsmicznego jest pozytywny,

p(X) - początkową ocenę prawdopodobieństwa znalezienia ropy, p (Y/X) - prawdopodobieństwo pozytywnego wyniku testu sejsmicznego, jeżeli pokłady ropy rzeczywiście istnieją. Innymi słowy, chodzi o niezawodność testu sejsmicznego,

p (Y/X„) - prawdopodobieństwo pozytywnego wyniku testu sejsmicznego, jeżeli pokłady ropy nie istnieją.    ^ y

Przechodząc do liczb mamy

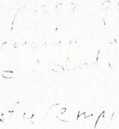
p (X) = 0,55

zatem V' > J

0    •> . '    ,    .    •    ? V • -7 ■ p L,

1    “    , c ' V \

p (X„) = 0,45

ęio . ■    ’

p (Y/X) = 0,822

p {Y/X„) = 0,178    roi' V

W efekcie

P (X/Y) =

0,55 x 0,822

0,822 * 0,55 +0,178 * 0,45

p{Y/X0 = 0,85

Zanim przejdziemy do obliczenia prawdopodobieństwa nieznalezieni; ropy w przypadku pozytywnego wyniku testup (X_n /F), prawdopodobieństw; znalezienia ropy w przypadku negatywnego wyniku testu p (X fY_n) ora-, prawdopodobieństwa nieznalezienia ropy w przypadku negatywnego wyniki testu p (X_n fY„), zwróćmy uwagę, że mianownik reguły Bayesa:

p (Y/X) *p(X)+p (Y/X_n) *p (X„)

12: