9 (1593)

fi n4*gfn>o- c*(^'nl) * Ci(t( n))=^tfc^c₂.)*(s(n)^%{(n)){prz\'imuiac (c**cj - e }^*(s(n)*tf n)

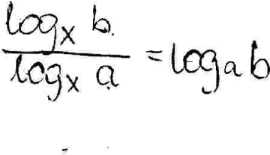
f(n)*g(n)= Ó(s(n)*i(n))c.n.d.

d) ^ reguła przechodni ości

z^n^RguO) i gcn)-0Cb(ii))

T: f(n)=0(h(ń))

D:

1)    f(n)KXg(n))^s>rstnięje takie „C|” należące do zbioru liczb rzeczywistych i istnieje takie n\ należące do zbioru liczb naturalnych

taki źe dla każdego n=>ni f(n)<= c,(g(n))

2) g(n)^j:iO(h(n))=>ismieje takie „Ci" należące do zbioru liczb rzeczywistych i istnieje takie n₂ należące do zbioru liczb naturalnych

taki że dla każdego n=>n₂ g(n)<= c_:(h(n))

Rn>'= ^i(g(n)><= Cj(ci(h(n)))=(C|.c,)*(b(n)) {przyjmując    = e }=c*(h(n)

istnieje takie „e” należące do zbioru liczb rzeczywistych i istnieje takie należące do zbioru liczb naturalnych taki że dla każdego n->n* f(n)= 0(h(n)) c.n.d.

2^ Określić złożoność obliczeniowa aigorybnu wyznaczania wartości wi&iómiańu dla przygaelków:(a) korzy stając bezpośrednio ze wzcru;(b) korzystając ze schematu Homera.

a)    algorytm wyznaczania bezpośrednio ze wzoru beęm

M _    . rfi) ,

VI .    C >. V ; /

for i:=1 to n do p : =x;

for j : = 1 to i-i do p:«p^T x; end for;

V*: = a{i)-prW; end for;

enc;

Badanie złożoności:

zakładamy operacje dominujące : mnożenie i dodawanie;

- wewnętrzna pętla for:

za    przejściem pętli zew. For ilość mnożeń = 1

zaprzejściem pętli zew. For ilość mnożeń - 2 i tak aż do n przejścia pętli zew. For ilość mnożeń = n-1 razem ilość mnożeń = 1 + 2 + 3 - 4 -r ... + n-1 = n(n-l)/2 ^k - zewnętrzna pętla for: ilość mnożeń « n ilość dodawań ~ n

razem złożoność obliczeniowa T(n)=n'fn-j-[n(n-l )/2]=n(n^3)/2=0(n”)

b)    korzystając ze schematu Homera beęin

W :« a [ n J ;

for l;=n-l down to 0 do W: - W*x, - a (i J ; end for;

end ;

Wyjaśnienie algorytmu:

W(x) = aW + Łn.iK¹¹'¹ + a_?.₂xⁿ'^;! -i-... + a,x + a* =

= (a,*"'¹    a_,__]x^r'’^: + a^.W' - ... + a,)x + a<) =

= ... = ((...(a^pc + Vi)x +    - + )x + a,)x + a*