Bez nazwy�

168

yj -y,

~y>g

( \

,    m-,

\+a —

m

(17.12)

lub po uwzględnieniu wzoru (17.3)

yj =y,

1 +

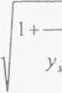
2h
/	\
	rn2
1 +a
\	^m\ )

(17.13)

Stosunek maksymalnego ugięcia wywołanego spadającym ciężarem do ugięcia jakie ten ciężar wywołuje, działając statycznie na konstrukcję, nazywamy współczynnikiem nadwyżki dynamicznej Kj. Mamy więc

y i

i +

2 h

y.

r    \

i ^,ni

\+a —

(17.14)

rn

Ponieważ ze wzrostem ugięcia zwiększają się odkształcenia i naprężenia, mamy

s_d=K_jes,    (17.15)

a_J=K_Ja_s.    (17.16)

Z analizy wzorów (17.12) do (17.14) wynika, że masa belki /ri₂ oraz jej podatność (dużey,) zmniejszają^. W przypadku, gdy masa spada z dużej wysokości, to znaczy, gdy h >>y_s, wartość ułamka jest duża w porównaniu z jedynkami stojącymi pod i przed pierwiastkiem. Po pominięciu jedynek we wzorze (17.12) i wyciągnięciu V! spod pierwiastka widzimy, że w tym przypadku A^jest proporcjonalne do prędkości bijaka w chwili uderzenia.

Jeśli h = 0, to Kj = 2. Ta wartość Kj opisuje nadwyżkę dynamiczną drgającej belki po nagłym zwolnieniu ciężaru dotykającego belkę, ale na niej nie spoczywającego. Drgania te zachodzą wokół położenia równowagi y, z amplitudąy,, to znaczy od 0 do 2y_s i stąd Kj = 2.

Aby obliczyć Kj ze wzoru (17.14), musimy uprzednio obliczyć a, korzystając ze wzoru (17.6). Uwzględniwszy, że /m = pA l (A - pole przekroju belki), mamy

\v¹{x)dx

a

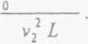
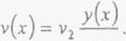
a =

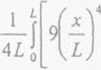
(17.17)

(17.18)

(17.20)

(17.21)

Założywszy, że kształty dynamicznej i statycznej linii ugięcia są podobne, prędkość dowolnego punktu belki opisuje równanie

y,

Po podstawieniu wzoru (17.18) do wzoru (17.17) otrzymamy:

\y\x)dx

a =-5—r-.    (17.19)

y}L

Przy uderzeniu w koniec belki wspornikowej, uwzględniwszy wzory (17.1) i (17.2), otrzymujemy:

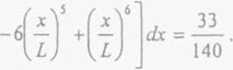
Gdy bijak uderza w dowolny punkt belki wspornikowej, określony przez współrzędną x = tjL, wówczas

105-105^-r35^² -2^³ 14077²

17.2. Opis zjawiska uderzenia po osiągnięciu maksymalnego ugięcia

Po osiągnięciu ugięcia yj, gdy energia kinetyczna bijaka została całkowicie wyczerpana, następuje ruch belki i bijaka w górę kosztem energii sprężystej zgromadzonej w ugiętej belce. Energia kinetyczna układu ponownie wzrasta i osiąga maksimum, gdy ugięcie zmaleje do y,. Wspólny ruch belki i bijaka trwa jednak nadal kosztem energii kinetycznej. W momencie gdy belka zacznie wyginać się w górę, ruch belki będzie hamowany przyciąganiem ziemskim i siłami sprężystości belki, a ruch bijaka w górę będzie hamowany tylko przyciąganiem ziemskim. Wynika z tego, że opóźnienie końca belki będzie większe niż bijaka, w rezultacie czego bijak oderwie się od końca belki. Wyginanie się belki w górę będzie trwało aż do wyczerpania energii kinetycznej samej belki. Maksymalne ugięcie belki w górę