CCF20110129030

a) b)

-q    +q    -q    +q

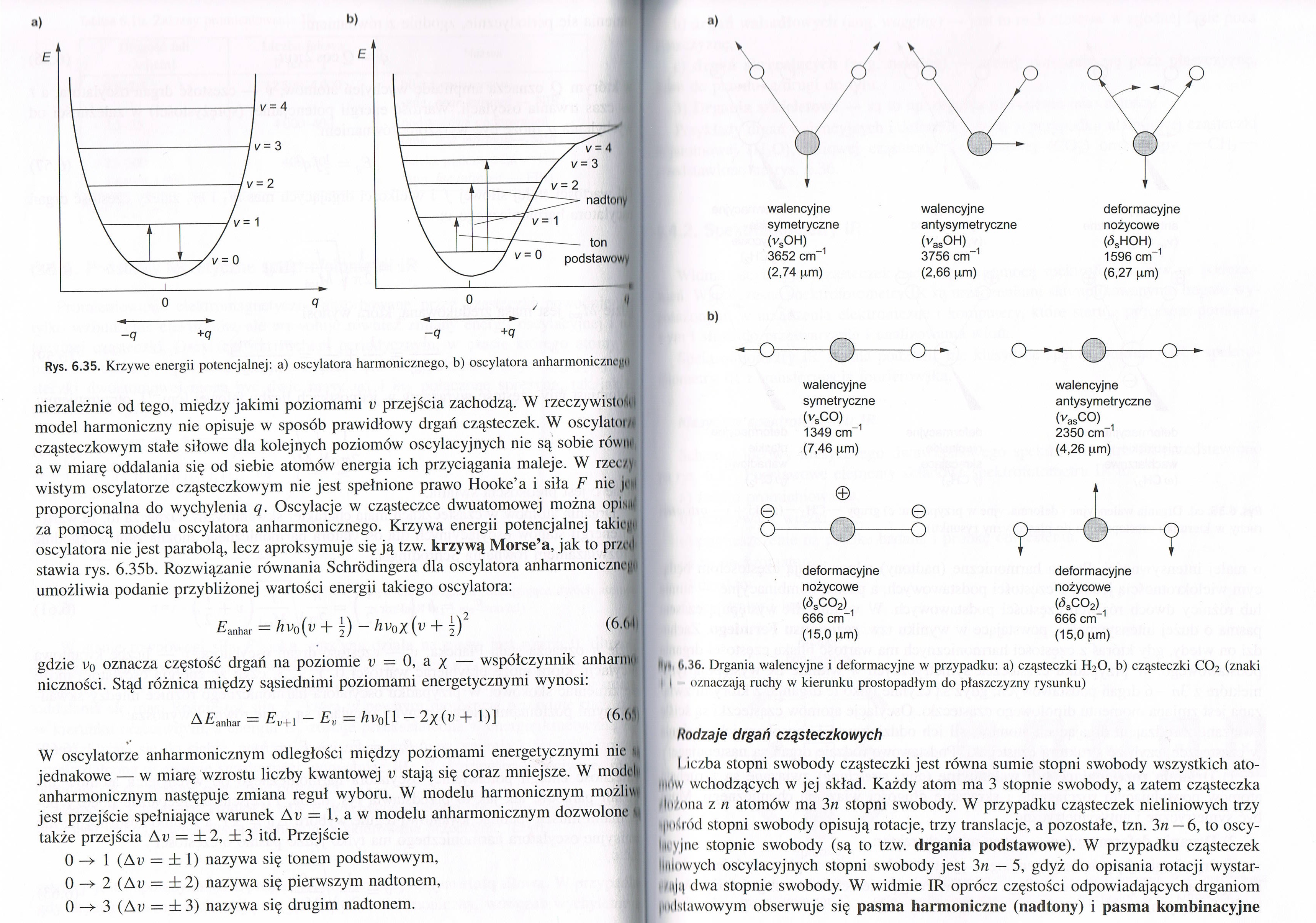
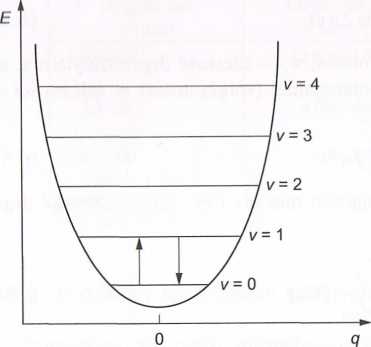
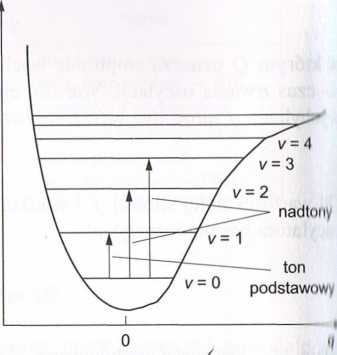
Rys. 6.35. Krzywe energii potencjalnej: a) oscylatora harmonicznego, b) oscylatora anharmonicznq>t.

niezależnie od tego, między jakimi poziomami u przejścia zachodzą. W rzeczywisto¹.! model harmoniczny nie opisuje w sposób prawidłowy drgań cząsteczek. W oscylator cząsteczkowym stałe siłowe dla kolejnych poziomów oscylacyjnych nie są sobie rówm a w miarę oddalania się od siebie atomów energia ich przyciągania maleje. W rzec/-, wistym oscylatorze cząsteczkowym nie jest spełnione prawo Hooke’a i siła F nie je proporcjonalna do wychylenia q. Oscylacje w cząsteczce dwuatomowej można opisiii za pomocą modelu oscylatora anharmonicznego. Krzywa energii potencjalnej takiep oscylatora nie jest parabolą, lecz aproksymuje się ją tzw. krzywą Morse’a, jak to przed stawia rys. 6.35b. Rozwiązanie równania Schródingera dla oscylatora anharmonicznq» umożliwia podanie przybliżonej wartości energii takiego oscylatora:

£anhar = hv₀(v + 5) - /iV()X (« +    (6.<>'l

gdzie p₀ oznacza częstość drgań na poziomie u — 0, a / — współczynnik anhanm niczności. Stąd różnica między sąsiednimi poziomami energetycznymi wynosi:

AE_anhar = E_v+\ ~ E_v = hv₀[ 1 - 2x(v + 1)]    (6.(0

W oscylatorze anharmonicznym odległości między poziomami energetycznymi nie 1> jednakowe — w miarę wzrostu liczby kwantowej v stają się coraz mniejsze. W modeli anharmonicznym następuje zmiana reguł wyboru. W modelu harmonicznym możliw jest przejście spełniające warunek Av = 1, a w modelu anharmonicznym dozwolone także przejścia Au = ± 2, ± 3 itd. Przejście

0 —y 1 (Au = ±l) nazywa się tonem podstawowym,

0->2(Au = ±2) nazywa się pierwszym nadtonem,

0 —»• 3 (Au = ± 3) nazywa się drugim nadtonem.

o-O-o-*-

o—-

walencyjne

antysymetryczne

(v_asCO)

2350 cm'¹ (4,26 (im)

b)

walencyjne

symetryczne

(v_sOH)

3652 cm^-1 (2,74 pm)

walencyjne

antysymetryczne

(v_asOH)

3756 cm^-1 (2,66 urn)

deformacyjne

nożycowe

(<5_sHOH)

1596 cm^-1 (6,27 (im)

walencyjne

symetryczne

(v_sCO)

1349 cm'¹ (7,46 (im)

©

Ó

O

©

o

deformacyjne

nożycowe

(<5_sC0₂)

666 cm ¹ (15,0 (im)

?

deformacyjne

nożycowe

(<5_sC0₂)

666 cm ¹ (15,0 (im)

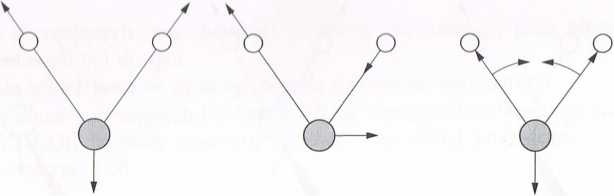
"i> <»-36. Drgania walencyjne i deformacyjne w przypadku: a) cząsteczki H₂0, b) cząsteczki C0₂ (znaki i oznaczają ruchy w kierunku prostopadłym do płaszczyzny rysunku)

Rodzaje drgań cząsteczkowych

I .iczba stopni swobody cząsteczki jest równa sumie stopni swobody wszystkich ato-"»Hv wchodzących w jej skład. Każdy atom ma 3 stopnie swobody, a zatem cząsteczka In/ona z n atomów ma 3« stopni swobody. W przypadku cząsteczek nieliniowych trzy pttńród stopni swobody opisują rotacje, trzy translacje, a pozostałe, tzn. 3n-6, to oscy-"Vjne stopnie swobody (są to tzw. drgania podstawowe). W przypadku cząsteczek Milowych oscylacyjnych stopni swobody jest 3n - 5, gdyż do opisania rotacji wystar-H|i| dwa stopnie swobody. W widmie IR oprócz częstości odpowiadających drganiom , .ilsiawowym obserwuje się pasma harmoniczne (nadtony) i pasma kombinacyjne