CCF20110307040

A
ZADANIE 4

W hurtowni owoców tropikalnych przeprowadzono analizę zmian sprzedaży łącznie trzech wybranych gatunków owoców: cytryn, pomarańczy i bananów w dwóch wybranych miesiącach: marcu i czerwcu. Wyniki badań empirycznych przedstawia tablica:

owoce	marzec		maj_
	ilość (w kg)	cena	ilość (w kg)	cena
cytryny	400	4,5	400	4,8
pomarańcze	900	3,8	500	6,5
banany	700	2,7	850	3,3

Ocenić zmiany wartości cen i ilości sprzedawanych owoców. Stwierdzić, co w silniejszym stopniu wpływa na zmiany wartości sprzedaży - zmiana cen czy zmiana ilości.

Rozwiązanie

Ze względu na potrzebę rozpatrywania łącznie zmian wszystkich (tzn. trzech) gatunków owoców w zakresie wartości, cen i ilości w miejsce indywidualnych mierników dynamiki wykorzystujemy mierniki agregatowe.

Mają one postać: agregatowy indeks wartości

2>_jn

j=l k

jo

Z W

j=l

gdzie:

Wj„ -wartość „j”-tego elementu agregatu (zespołu elementów podlegających zmianom) w momencie bazowym (wcześniejszym w sensie chronologicznym)

Wj„ - wartość „j”-tego elementu agregatu w momencie badania (chronologicznie późniejszym)

agregatowy indeks cen:

IPjngj

ip =

;i) Laspeyresa:

ZPjnflj

z; p _ioq i

li) Paaschego:

iPiog,

agregatowy indeks ilości:

a)    Laspeyresa:

[I- _    Pjo^Cli"

'q 'T-i

LPjo^io

b)    Paaschego:

r /* ^ P jn^Cl jn

¹Q V'

Z

gdzie odpowiednio:

pjo, Pjn - ceny „j”-tego elementu-agregatu w momencie wzorcowym qjo, qjn - ilości „j”-tego elementu agregatu w momencie badania

Indeksy agregatowe wartości, cen i ilości Laspeyresa i Paasche’go pozwalają na oceny zmian wartości z uwzględnieniem przyczyny tych zmian lub bez podania przyczyn.

Łączne zmiany cen i ilości ustalamy za pomocą indeksów Fischera (odpowiednio cen i ilości), czyli średnich geometrycznych indeksów agregatowych Laspeyresa i Paasche’go.

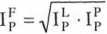
i

a

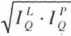
W naszym przypadku obliczanie warto przeprowadzić w pomocniczej tablicy: