CCF20120509090

1IW ii. ivu/.ni<{/.<iiiia i imi|#uwicu#,i V s. Dynamika cieczy rzeczywistych 31

Objętościowe natężenie przepływu

5.1.8. Warunkiem spełnienia podobieństwa dynamicznego przepływów jest równość liczb Reynoldsa, czyli

h

2

Q = 2jvbdz,

o

natomiast średnia prędkość przepływu

Re_w — Re₀,

Udzie

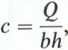
ji

2

/ulem

Re_w =    oraz Re₀ =    ,

zatem

c_wD c₀D

l‘niiieważ

2 Jud z

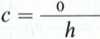
(HI

4<2_W    4<2o

c„, -    ~ oraz c_n =

Po podstawieniu zależności (7) do wzoru (8) otrzymamy:

nD

⁰ nD²'

oi Inn

fi.

2

C =

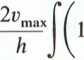
0

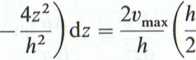
2

o ^? inu\

4QJ> __ 4Q₀D

kD²v„, nD²v_n

lub

2Aph² Aph² 3 8vpl 12vpl

Uwaga: Niniejszy przykład można również rozwiązać za pomocą równali Naviera-Stokesa.

l Matecznie natężenie przepływu oleju

Q₀ = Q_W~,

ii po podstawieniu wartości liczbowych,

5.1.7. Prędkość średnia przepływającego mazutu

^ = 0,005^ = 0,047 m³-s^_1.

c

^ĄQ.

nd² ’

M.9. Liczba Reynoldsa

Re =

cd

4 -0,001 7t(0,10)²

= 0,127

m-s

u nlijętościowe natężenie przepływu

Liczba Reynoldsa

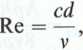
filiom

nd²

e = c—,

Re

0,127-0,10

6,2-10^-6

= 2048.

Re

4Q

ndv'

Obliczona wartość liczby Reynoldsa jest mniejsza od Re_kr = 2300. W związku tym, przepływ mazutu możemy uznać za laminarny.

/ tiNlutniej zależności wynika, że zwiększając średnicę przewodu, zmniejszamy liczbę Krynoldsa, a tym samym możemy otrzymać przepływ laminarny.