CCF20130109019

stąd

a₀= 28°25'.

Główne centralne momenty bezwładności obliczamy ze wzoru (2.16). Otr/y mujemy:

I_max =I__V| = ^-(95,48 + 73,24)+^(95,48 - 73,24)² + 4(-17,02f =104,69 cm'¹, I_min =1, = -^(95,48 + 73,24)-^V(⁹⁵>⁴⁸ - 73,24)² + 4(-17,02)² - 64,03 cm⁴.

Ad b) położenie środka ciężkości figury jest w tym przypadku znane, wobec lepu prowadzimy osie układu y₀» Zo o początku w środku ciężkości.

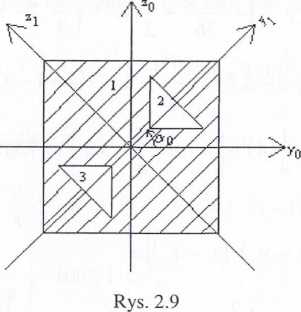
Dzielimy figurę na kwadrat i dwa trójkąty.

Obliczamy osiowe momenty bezwładności figury oraz moment dewiacji wzglę dem osi centralnych y₀» Zo jako różnicę momentów całej figury i wyciętych ulwo rów o kształcie trójkątów. Podobnie, jak w poprzednim przykładzie, korzystamy z twierdzenia Steinera i tablicy 1. Mamy:

k,=ŻL ^+AkJ]=

<•=i

10^4	3 • 3^3 1 „	r, i )	2		3 • 3^3 1	( i v
—	-+ --3-3			—	+ -3-3
12	36 2	l ^3 J			36 2	l ^3 J

= 792,83 cm⁴,

i i

K)'«	3^3 • 3 1	r i ^	2		3^3 • 3 1 0	i 1 ^	2"
	+ • 3 • 3			—	-+ —-3-3	-1---3
1 ’	36 2	l ^3 >			36 2	l ^3 J

/92,83 cm⁴,

¹ I ¹ • nic głównych centralnych osi bezwładności określamy z zależności (2.15),

nn

'M

2(- 33,75)

792,83 - 792,83

K _Ł ,    TT

9l_h >    , stąd a = —.

2    4

......11 głównych centralnych momentów bezwładności wynoszą odpowiednio

hi ' Ui):

I,...    1,    -(792,83 + 792,83) +    (792,83 - 792,83)² + 4(— 33,75)² =

826,58 cm ,

_-

I...... I ¹ (792,83 + 792,83)--V(792,83-792,83)² +4(-33,75)²

* 2 ¹ 2 / 59,08 cm .

I

i-t

3² • 3²    1

-——+ —• 3 ■ 3 72    2

3² ■ 3²    1

-——+ —• 3 • 3 72    2

1+--3 1 +

3-3

/J

+

-1-^-3

/j

:-33,75 cm⁴.

1

I','VM Al) 5

I Mn |n . i kroju złożonego z profili walcowanych, jak pokazano na rysunku 2.10, il.    |uitożcuic głównych centralnych osi bezwładności oraz obliczyć główne

Hihiliir momenty bezwładności.