CCF20130109022

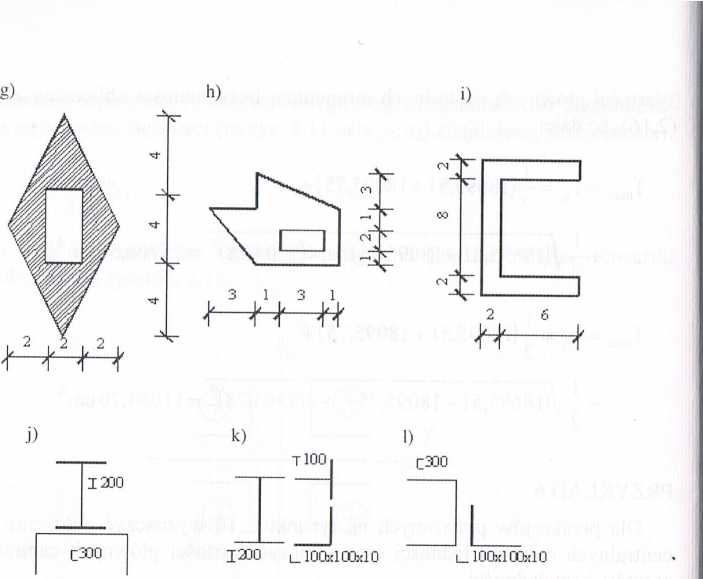
Rys. 2.14

Odpowiedzi do przykładu 6

Przykład	IjVo [cm^4]	Izb [cm^4]	I.VoZ() [cm^4]	a [°]	^max [cm ]	^min [cm |
a	345,65	248,57	242,14	-39°19’	544,07	50,15
b	67,5	67,5	-33,75	45°	101,25	33,75
c	290,67	162,67	-120	30°57’	362,67	90,67
d	42,67	42,67	-	-	42,67	42,67
e	896	464	-480	32°53’	1206,36	153,64
f	878,15	878,15	-127,16	45°	1005,31	750,99
g	205,33	51,33	-	-	205,33	51,33
h	78,37	102,33	-11,63	-22°04’	107,05	73,65
i	896	272	-	-	896	272
.i	6077,13	8147	-	-	8147	6077,13
k	5023,07	2849,97	307,66	-7°54’	5065,79	2807,25
1	10354,23	1113,02	-1076,48	6°33’	10477,96	989,29

.1. SIŁY PRZEKROJOWE

.1.1. DEFINICJE SIŁ PRZEKROJOWYCH

Rozważmy dowolny element, na przykład pręt o zwartym przekroju, obciążony układem uogólnionych sił zewnętrznych P_t (i = 1,2,3,...,n), pozostających w równowadze (rys. 3.1).

z

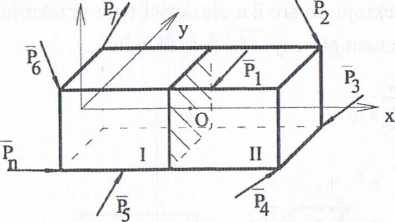
Rys. 3.1

Przetnijmy myślowo rozpatrywany element płaszczyzną poprzeczną, prostopadłą do osi x (oś pręta). Płaszczyzna ta dzieli pręt na dwie części oznaczone na rysunku 3.1 jako część I i II.

Układ sił zewnętrznych /} został tym samym podzielony na dwa układy: P_n

i P,n . Dla zapewnienia równowagi sił działających na każdą z części pręta konieczne jest uwzględnienie wzajemnego oddziaływania oddzielonych części na siebie. Siły wzajemnego oddziaływania są rozłożone w przekroju pręta w sposób ciągły.

Oznaczmy przez Wj siły oddziaływania części II pręta na część I i przez W„ siły oddziaływania części / pręta na część II. Dla każdej części pręta mamy zależność:

(3.1)

P„+W,= o, P_m+.W_n= 0.

7, powyższego wynika, że:

W, =-P_n oraz W_u=-P_m.

Ponieważ dla układu sił działających na pręt jest spełniony warunek równowagi