DSC00009 (29)

IP

<y

IWS 9jjn n 3/

.'^{Ti a}, -;^aivi + y• ^arM + a₀• In = 0]+a, • [n = 1].

>Nskaż poprawne stwierdzenie:

{12^ <fia dowolnych € P zachodzi p |m A p |n => p jm • n;

\B) na podstawie Maiego Twierdzenia Fermata zachodzi: n¹⁰¹ s n (mod 101) dla każdego tl # k -101. gdzie keZ;

S je£& TT^ € N są liczbami pierwszymi, to przynajmniej jedna z liczb fTI • HJ— jest nieparzysta; 2< j \J 4    n

po wykonaniu zmodyfikowanego algorytmu Eukfidesa można otrzymać liczby U, V spełniające równanie ~1 = U-31 + V-10Q; p. ż Podstawowego Twierdzenia Arytmetyki wynika, że 24 == 4 • 6.

4. Dta kongruencji 4 • X = 3(mod 6) wskaż poprawne zdanie:

X = 3 jest rozwijaniem kongruencji;

S) ponieważ NWD(4;6) = 2 oraz 3 nie dzieli się przez 2, więc kongruencja nie ma rozwiązania; ponieważ NWD (3; 6) = 3 oraz N WD (4; 6) = 2, więc kongruencja nie ma rozwiązania;

S X = 3 + k-6 dla k € Z jest rozwiązaniem kongruencji;

□ ponieważ NWD(3;4) = 1, to kongruencja ma dokładnie nieskończenie wiele rozwiązań.

5. Zaznacz poprawne zdania:

□ funkcja 4-z-f 8z jest funkcją tworzącą ciągu odpowiadającego zbiorowi (4; 8);

(q) a d Hb-d(modd*n)oa»b(mocln) dla d*0 ;

(2/ rn he n(modk) o m* * n* mod(k) dla a e N;

Q rozwiązanie kongruencji m • X s a(mod n) istnieje tylko wtedy, gdy NWD(m ;n) = 1;

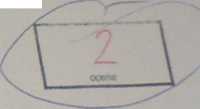
(OJ liczba wszystkich podzbiorów zbioru z powtórzeniami (2 * 2; 3 * 3} jest równa 12. I

3

odpowiedzi błędne

odpowiedzi poprawne

brak odpowiedzi poprawnych