DSC00591 (4)

Mb

■

Kolokwium 2 z przedmiotu Ekonometria (Badania operacyjna)

(przygotował dr Michał Karpuk)

S

*

<£L

LCi.

Grupa

ł(

Stanowisko No

/. (1 pkt^Wab/ic^odan^rzepustowofc^tte^iec^N^ocIstawi^ablicy narysuj graf siad    f

2. (1 pkt) Zorganizuj 3 potoki od punktu 1 do punktu Gi oblicz mocy oddzielnych potoków i całej sieci. jt fspiet) Zmaksymalizuj potok od p. 1 do p.6 metodą Ford'a-Fulcerson 'a w sieci i znajdź cięcie z minimalną przepusto-

W/ ^rt2 / ^r13 i ^r15 i ^rie / ^r23 j ^r24	I f i	I ^rx t	I ^r* i	I ^r« i	/ rm I
f 4 / 1 / 10 i 9 / 6 / 8 I		zn	^9 I	' * i	^8 I

Zadanie 2 Macierz gry dwuosobowej o sumie zero jest zapisana w tabeli 1. (1 pkt) Oblicz dolną i górną cenę gry.

2 (2 pkt) Zapisz zadanie planowania liniowego dla gracza B (model dualny)

3. (3 pkt) Narysuj wykres dla zadania dualnego, zaznacz dziedzinę dopuszczalnych rozwiązań i punkt optymalny.

	i±_	r ** i
/" I	11	f « ^1
ULI	*
Ui I	jj	—^3 <

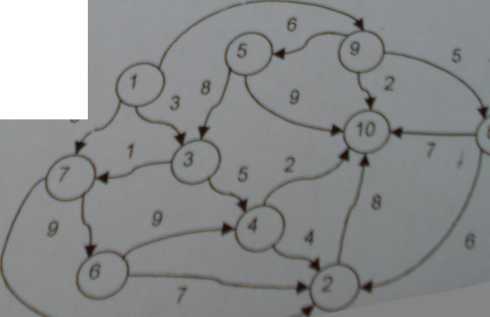
Zadanie 3. Na rysunku podana sieć dróg łączących punkty 1 i W Tablica zawiera planowany czas podróży pot Punktami (w godzinach). Numer wiersza wskazuję punkt startowy, numer kolumny punkt docelowy 1(1 pkt) Dla podanego grafu zapisz macierz zbieżności wierzchołków.

(1 pkt) Uporządkuj graf metodą Fułcerson'a.

(1 pkt) Znajdź najdłuższy czas podróży od p. 1 do p 10.

1 Pkt) Znajdź najdłuższy czasy podróży od pozostałych punktów do p. 10.

Pkt) Przyjmując (oczekiwane - (planowane i 9=2 zapisz funkcję    _c

gęstości prawdopodobieństwa ^f Pkt} Obtocz prawdopodobieństwo podróży od 1 do^ł10 w ^gzpsu a) od O do 5 godzin, b) od 25 do 30 godzin *^<*^ar*oo*e/est najbardziej oczekiwane?

tędzy