DSC00828 (6)

y- Hi

(17)

Warunek symetrii odbiornika

Z1-Z2-Zj,

(18)

co oznacza

|z,|- |Zj| =|Zj I- |z| oraz <pi = <Pz - <Pj “ <P

(19)

a)    i

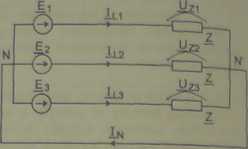
Rys.56. Obwód symetryczny trójfazowy czteroprzewodowy typu gwiazda-gwiazda Na podstawie I i II prawa Kirchhoffa otrzymuje się:

!n-!li^+1l2 +Iu	(20)
Ei-ZtŁi+yN	(21)
Ęj^ZjIu + Un	(22)
Ę3«Za!u^+Ł!N	(23)

Z układu równań: (21), (22), (23) wyznacza się napięcie między punktamiN iN.

(24)

z sieci czteroprzewodowej

„ E.L+ŁIi *ŁŁ X,+Xi+X,+Ł

Dla obwodu symetrycznego: Y| = Y2 = Yj ■ Y zasilanego przy Yk“<jc wzór (24) przybiera postać:

B.X+ĘrY₊E,X a+Es+Ł)! a

U N =    ---------- ' '    .. .............06 O

3X + Xk    3Y+Y_m

Zgodnie z podaną wcześniej zależnością (12) suma napięć fazowych symetrycznego źródła zgodnego jest równa zero, stąd U* dla symetrycznego odbiornika trójfazowego połączonego w gwiazdę równa się zero.

Dla symetrycznego odbiornika trójfazowego połączonego w gwiazdę zasilanego z sieci czteroprzewodowej otrzymamy:

ii-	-Uzi-Uli	&	— Uzz “Uli	Ej-Uzj-Uu	(26)
Ili	19,, - ~ - Uzi	Y,	ka-^ki	lu->ki	07)

In = Ili ⁺ Ili ^łlu* ( 1 + a^ł + a) Ili “

lN=lL1 ⁺ iu⁺iL3 = 0

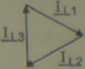
Rys. 5.7. Wykres wskazowy dla odbiornika symetrycznego o charakterze indukcyjnym połączonego w gwiazdę zasilanego z sieci czteroprzewodowej

Na postawie wykresu wskazowego oraz definicji napięcia międzyprzewodowego

Ulu = Uli - Uu Ulzj ■ Uu ' Uu Uui “ Ulj * Uli

1UluI = IUu3| = 1Ul3iI“1Ui-I    &⁹⁾

suma

Ulu + Uui + _Uui = 0    (30)

Trójkąt stworzony z dwóch napięć fazowych i między przewodowego jest trójkątem równoramiennym.

j§

= cos 30® cos 30° = ~~ ,

Uu    2

.(1 -I-j£ *

2 ^J 2

-i+4

2 2

Mu

o

an

75