74

(17)

Y- | Y | e'ⁱ⁹

Warunek symetrii odbiornika:

Zi = Z₂ = Z₃,    (18)

co oznacza

|Z||= IZ₂1 =|z₃ |= IZ l    oraz cpi = c?2 = <P3 = <p    (19)

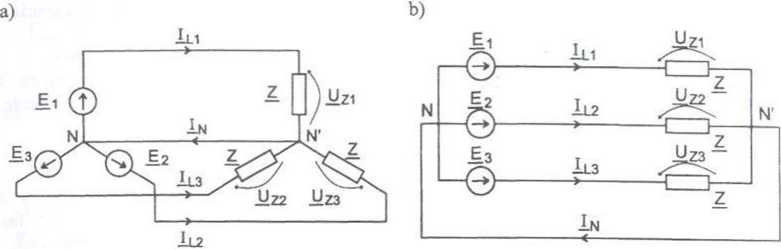
Rys.5.6. Obwód symetryczny trójfazowy czteroprzewodowy typu gwiazda-gwiazda Na podstawie 1 i II prawa Kirchhoffa otrzymuje się:

In = Ili + Il2 + Il3	(20)
E1 = Zi Ili + Un	(21)
E 2 = Z2 Il2 + Un	(22)
E3 = Z3 Il3 + UN	(23)

Z układu równań: (21), (22), (23) wyznacza się napięcie między punktami N i N.

(24)

z sieci czteroprzewodowej

(25)

u _ E.X,+e_;y₂ + ę₃y₃ -^N Ł+^+Ł+Y*

Dla obwodu symetrycznego: Yi = Y₂ = Y3 = Y zasilanego przy Yn = oc wzór (24) przybiera postać:

_v _ e.y+ę₂y+e₃y    (E|+E₂+E₃)Y

3Y + Y_n    3Y+Y_n

74

Zgodnie z podaną wcześniej zależnością (12) suma napięć fazowych symetrycznego źródła zgodnego jest równa zero, stąd Un dla symetrycznego odbiornika trójfazowego połączonego w gwiazdę równa się zero.

Dla symetrycznego odbiornika trójfazowego połączonego w gwiazdę zasilanego z sieci czteroprzewodowej otrzymamy:

In - Ili ⁺ Il2 + Ii.3 ~ (1 + a² + a) Ili =

Hi - Uzi - Uli E2	= Uz2 = uU2	E3 - Uz3 - Ul3	(26)
UZI Iu= = =Uzi Y,	lu ^= a^2 łu	Il3 ^= a Ili	(27)

Rys. 5.7. Wykres wskazowy dla odbiornika symetrycznego o charakterze indukcyjnym połączonego w gwiazdę zasilanego z sieci czteroprzewodowej

Na postawie wykresu wskazowego oraz definicji napięcia międzyprzewodowego

Ul12⁼ Uli-Uu Ul23 - Ul2-Hi.3 Ul31 ~ Ul3 ' Hu

|Ul,2| = |Ul23| = |Uu.| = |U_p|    (29)

suma

Uli2 ⁺ Ul21 ⁺ JJ.L31 ⁼ o    (30)

Trójkąt stworzony z dwóch napięć fazowych i międzyprzewodowego jest trójkątem równoramiennym.

ł^u

= cos 30° cos 30° =2^-,

Hu    ²

I

75