DSC02564 (3)

466 psychologia^

466 psychologia^

to

(100, 0) i (0, 100). Jeżeli natomia^Unkl

pierwszego uczestnika udziały ₀pj_s

Hiy

WCJ

czterofe

cjonalny. Jedynie taki podział, który nie może już być korzystniejszy dla żadnego uczestnika bez uszczuplania zysku innego uczestnika, może zostać uznany za racjonalny. Mówi się o takim podziale, że jest on optymalny w sensie Pareto.

3. Warunek niezależności rozwiązania od liniowego przekształcenia skali użyteczności. Postulat ten zapewne brzmi nieco technicznie, ale w istocie jest prosty i całkowicie naturalny. Wyobraźmy sobie, że jeden z uczestników liczy swoje pieniądze w złotówkach, a drugi w euro. Pokazuje to rycina 15.1. Status quo (kiedy żaden z uczestników nie otrzyma niczego) znajduje się w punkcie (0,0). Jeżeli obszar negocjacji (optymalny w sensie H szemy dla obu uczestników w złotó it reprezentuje go odcinek łączaci !H

ii

złotówkach, a dla drugiego nie niższym nominale - euro, to obszar gocjacji reprezentuje odcinek łączacv n,? kty (25,0) i (0,100).    ^p "

Jest zrozumiałe, że podział nie p_ow nien zależeć od tego, czy uczestnik lyj o nim w złotówkach czy w euro, Rozwj; zanie powinno być w obu wypadkach |$ nakowe. Gdyby na przykład „myśląc w z|₀ tówkach”, uczestnicy przyjęli rozwiąż nie (50,50), to „myśląc w euro” musielibi przyjąć rozwiązanie (12,5; 12,5), gdyby za

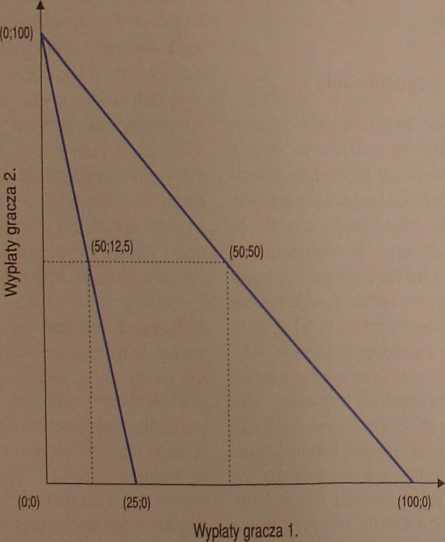
Obszar i wyniki negocjacji (w złotówkach i w euro) dla uczestników podziału ■■■■■ Rycina 15.1 ■■■■■■

pierwszy „myślał w złotówkach”, a drugi w „euro”, to musieliby przyjąć rozwiązanie (50; 12,5).

4. Warunek niezależności rozwiązania od możliwości bez znaczenia. Przypuśćmy, źe jakimś osobom dano do podziału 100 zł, pozostawiając im swobodę wyboru sposobu podziału, ale z zastrzeżeniem, że każdy uczestnik musi dostać co najmniej 5 zł. Czy ograniczenie to może mieć jakiś wpływ na końcowe rozwiązanie? To zależy. Może ono mieć znaczenie, jeżeli uczestnicy w ogóle rozważają taką możliwość, że któryś z nich mógłby dostać mniej niż 5 zł. Przypuśćmy jednak, że można ustalić, iż te same osoby, kiedy otrzymują do podziału 100 zł bez żadnych ograniczeń, nie kończą negocjacji na podziale, który dawałby którejś z nich mniej niż 5 zł. Jeżeli tak, to rozsądny wydaje się postulat, że w takim przypadku uczestnicy powinni przyjąć taki sam podział niezależnie od tego, czy ograniczenie zostało wprowadzone, czy nie. Można po prostu sądzić, że skoro uczestnicy tak czy owak nie wykorzystują pewnych możliwości podziału, to wykluczenie owych możliwości niczego nie powinno zmieniać.

Przedstawione warunki są ciekawe z dwóch powodów. Po pierwsze, pokazują możliwe błędy, jakie można popełnić w gorączce negocjacji. Na przykład uczestnicy negocjacji nie zawsze zachowują warunek optymalności Pareto (o którym będziemy jeszcze mówić nieco dalej) i dochodzą do rozwiązań, które można poprawić przynajmniej dla jednej strony, nic nie odbierając (albo nawet dodając) drugiej stronie. Mogą też powoływać się na możliwości, które są bez znaczenia itd.

Drugi, logiczny, pożytek z przytoczonych postulatów wyprowadził John Nash (1951), który matematycznie wykazał, że omówione cztery warunki racjonalności gwarantują znalezienie dokładnie jednego rozwiązania problemu podziału. Takiego

rozwiązania, które powinno zostać przyjęte przez racjonalnych uczestników i powinno być odporne na zmiany (być w równowadze). Rozwiązanie to, w abstrakcyjnej postaci, jest następujące:

Racjonalny jest taki podział, który maksymalizuje wartość iloczynu:

(U-u₀)(V-vJ

gdzie:

U - to satysfakcja pierwszej osoby z podziału (jej miara użyteczności), u₀ - to satysfakcja pierwszej osoby z jej status quo,

V - to satysfakcja drugiej osoby z podziału (jej miara użyteczności), v₀ - to satysfakcja drugiej osoby z jej status quo.

Innymi słowy, racjonalny jest taki podział, który przynosi największy iloczyn przyrostów miar użyteczności obu uczestników podziału, kiedy przechodzą oni z punktu status quo do uzgodnionego podziału.

Przybliżmy nieco tę abstrakcyjną koncepcję. Jak mogłaby wyglądać rozmowa między dwiema osobami, którym dano do podziału 100 zł? Powiedzmy, że rozpoczynający negocjacje pierwszy uczestnik mógłby wpaść na pomysł podziału (90, 10), czyli 90 zł dla siebie i 10 zł dla partnera. Mógłby to wyrazić tak:

Mam propozycję (90,10) i dobrze zrobisz, jeśli ją przyjmiesz, bo ja nie ustąpię i wtedy nie otrzymasz nic.

Czy argument ten odniesie skutek? Raczej nie, bo drugi uczestnik może odpowiedzieć tak:

Nie strasz, nie strasz! To prawda, że odrzucając twoją propozycję, nic nie dostanę i w ten sposób stracę, ale zauważ,